Качество регулирования в статических и астатических системах в установившихся режимах

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра РП и РПУ

Лабораторная работа № 1

по курсу «Радиоавтоматика»

Тема:Качество регулирования в статических и астатических системах в установившихся режимах.

Факультет: РЭФ

Группа: РТ5-91                                      

Студент: Есауленко К.Е.

Преподаватель: Лявданский С.Е.

Новосибирск 2012

Цель работы: Исследование качества регулирования в статических и астатических системах при различных регулирующих воздействиях.

С чего нужно начать?! Во первых надо понимать что понимают под качеством регулирования, а это есть форма и величина ошибки регулирования, которая является разностью между входным воздействием на систему и выходной функцией системы, т.е. её результатом регулирования. Чтобы понять, что к чему следует нарисовать структурную схему системы, а по ней продолжать дальнейшие действия.

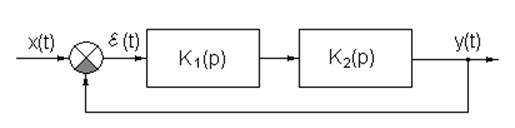
Рис.1 Структурная схема системы

Здесь - входное воздействие, - выходная функция системы, - ошибка регулирования.

Начнем со статической системы. Она состоит из двух инерционных звеньев.

Передаточная функция для статической системы имеет следующий вид

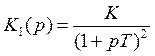
Теперь посмотрим, что произойдет, если будем подавать на её вход различные регулирующие воздействия.

1.1)  Постоянное воздействие

В этом случае у нас К=10, Т=0.1, К2(р)=1.

       

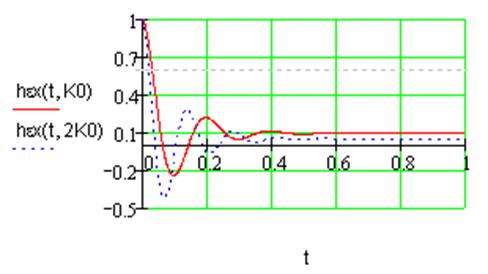
Рис.2. Переходная характеристика ошибки регулирования при постоянном воздействии

1.2)  Линейно растущее входное воздействие: .

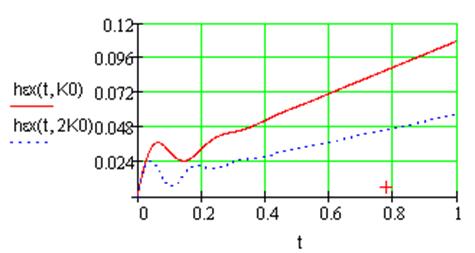
Рис.3. Переходная характеристика ошибки регулирования при линейном воздействии

1.3)  Параболическое входное воздействие: .

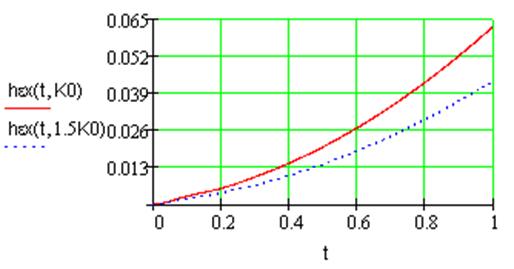
Рис.4.Переходная характеристика ошибки регулирования при параболическом воздействии.

По полученным переходным характеристикам ошибки можно сделать следующие выводы

1)  Порядок переходной характеристики ошибки регулирования совпадает с порядком входного воздействия;

2)  При увеличении коэффициента усиления системы уменьшается величина ошибки регулирования.

2. Астатическая система первого порядка состоит из одного интегрирующего и одного инерционного звеньев.  Передаточная функция такой системы имеет вид:

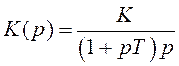
2.1. Постоянное входное воздействие: .

                                        

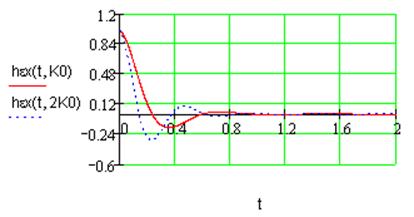
Рис.5. Переходная характеристика ошибки регулирования при постоянном воздействии.

2.2. Линейно растущее входное воздействие: .

   

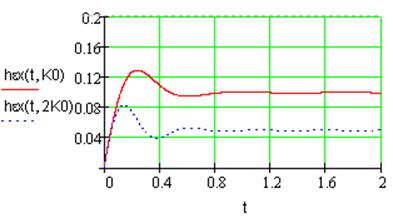
Рис.6. Переходная характеристика ошибки регулирования при линейном воздействии.

2.3. Параболическое входное воздействие: .

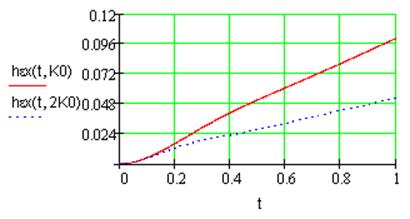
Рис.7. Переходная характеристика ошибки регулирования при параболическом воздействии.

На основе анализа рис. 5-7 можно сделать следующие важные для астатической модели первого порядка выводы:

1)  порядок переходной характеристики  ошибки регулирования для астатической системы первого порядка на единицу меньше порядка входного воздействия, таким образом, в рамках такой системы можно получить нулевую ошибку регулирования для постоянного воздействия при любом коэффициенте усиления системы и постоянную ошибку регулирования для линейно растущего входного воздействия;

2)  из рис. 6-7 видно, что при увеличении коэффициента усиления системы уменьшается величина ошибки регулирования.

2.  Астатическая система второго порядка состоит из двух интегрирующих и одного форсирующего звеньев. Передаточная функция такой системы имеет вид:

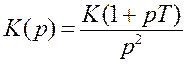
3.1.

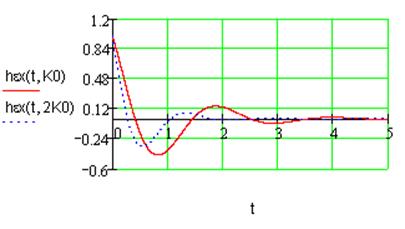
Постоянное входное воздействие: .

Рис.8. Переходная характеристика ошибки регулирования при постоянном воздействии.

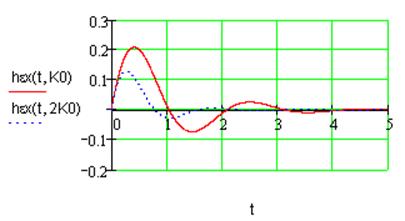
3.2. Линейно растущее входное воздействие: .

Рис.9. Переходная характеристика ошибки регулирования при линейном воздействии.

2.3. Параболическое входное воздействие: .

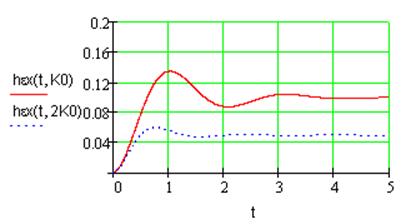
Рис.10. Переходная характеристика ошибки регулирования при параболическом воздействии.

На основе анализа можно сделать следующие важные для астатической модели второго порядка выводы:

3)  порядок переходной характеристики  ошибки регулирования для астатической системы второго порядка на две единицы меньше порядка входного воздействия, таким образом, в рамках такой системы можно получить нулевую ошибку регулирования для постоянного и линейно растущего воздействий при любом коэффициенте усиления системы и постоянную ошибку регулирования для параболического входного воздействия;

4)  из рис. 10 видно, что при увеличении коэффициента усиления системы уменьшается величина ошибки регулирования.

Таким образом, наблюдается очень интересная закономерность: с возрастанием порядка астатизма исчезают, начиная с S₀, коэффициенты ошибки, а в формуле  (1)исчезают слагаемые, начиная с первого. Однако не следует увлекаться астатизмом высоких порядков: интегрирующие звенья вносят фазовый сдвиг по -90 каждое. Поэтому уже при втором порядке астатизма возникают проблемы с устойчивостью системы. В связи с этим появляется необходимость вводить в систему дополнительные, так называемые корректирующие звенья. Тем не менее системы с порядком астатизма выше второго практически не используются. Однако не следует отчаиваться: уничтожение в формуле (1) даже первых двух слагаемых очень сильно уменьшает ошибку регулирования, так как эти слагаемые самые мощные и именно они вносят основной вклад в формирование ошибки регулирования (Честно, взял из методички для подготовки к лабораторным работам).

Также, я решил попробовать решить первую задачу аналитически, и найти ошибку так сказать вручную. Результат получился почти такой же, но конечно на компьютере это намного точнее, за счет разрядности. Далее для примера покажу, как я это делал.

Возьмем статическую систему, с постоянным воздействием

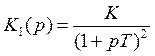
Далее следуя методичке для подготовке к лабораторным работам находим

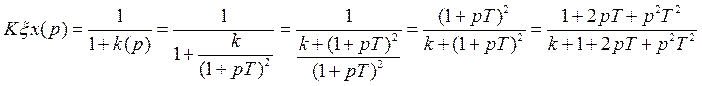
Коэффициенты характеристических полиномов

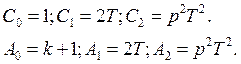
При подаче на вход системы постоянного воздействия

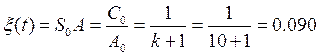
При подаче на вход системы линейно возрастающей функции

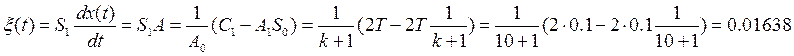
При подаче на вход системы параболического воздействия

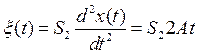
Дальнейшие выкладки очень объемны, но суть нахождения ошибки я уяснил.