Расчет автоматической системы

Содержание

Задание на расчетно – графическую работу……………………………………3

Исходные данные………………………………………………………………...3

1. Передаточная функция разомкнутой системы K(p)………………………...4

2. Структурная схема следящей системы. Определение названий всех

входящих в систему типовых структурных звеньев………………………………..4

3. Передаточная функция и дифференциальное уравнение замкнутой

системы………………………………………………………………………….……..4

4. Передаточная функция для ошибки от возмущающего воздействия……...5

5. Характеристический полином разомкнутой системы и вычисление

его коэффициентов…………………………………………………….………………5

6. Характеристический полином замкнутой системы и вычисление

его коэффициентов…………………………………………………………………….6

7. Анализ устойчивости системы по критерию Гурвица………………………6

8. Исследование устойчивости системы по критерию Михайлова

(метод чередующихся корней). Построение годографа Михайлова…………....... .7

9. Исследование устойчивости системы по критерию Найквиста.

Построение годографа Найквиста. Определение запаса устойчивости по модулю и по фазе…………………………………………………………….…….9

10. Нахождение ошибки регулирования x(t) и построение графика………....10

Литература……………………………………………………………………….12

Задание на расчетно-графическую работу.

1. Записать передаточную функцию разомкнутой системы K(p).

2. Зарисовать структурную схему системы, считая ее следящей. Дать название всех входящих в систему типовых структурных звеньев.

3. Записать передаточную функцию и дифференциальное уравнение замкнутой системы.

4. Записать передаточную функцию для ошибки от возмущающего воздействия.

5. Записать характеристический полином разомкнутой системы и вычислить его коэффициенты.

6. Записать характеристический полином замкнутой системы и вычислить его коэффициенты.

7. Произвести анализ устойчивости системы по критерию Гурвица.

8. Исследовать устойчивость системы по критерию Михайлова (метод чередующихся корней). Построить годограф Михайлова.

9. Исследовать устойчивость системы по критерию Найквиста. Построить годограф Найквиста. Определить запас устойчивости по модулю и по фазе.

10. Найти ошибку регулирования x(t) и построить график.

Исходные данные:

Передаточная функция замкнутой системы:

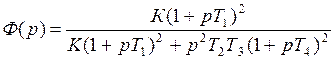
Коэффициенты передаточной функции:

К = 80,  Т₁ = 1.5 с.,  Т₂ = 2 с.,  Т₃ = 1.2 с.,  Т₄=0.2с..

Входное воздействие:

1. Передаточная функция разомкнутой системы K(p).

Запишем передаточную функцию замкнутой системы через передаточную функцию разомкнутой системы по материалам работы [4] (формула 1), затем, проведя несложные арифметические преобразования, получим K(p):

	(1)
	(2)
Разделим числитель и знаменатель выражения Ф(p) на
	(3)
Следовательно, учитывая (1), получим
	(4)

2. Структурная схема следящей системы. Определение названий всех входящих в систему типовых структурных звеньев.

Разобьем передаточную функцию К(р) на составляющие следующим образом:

(5)

Теперь мы можем зарисовать структурную схему:

Рисунок 1. Структурная схема следящей системы.

Как видно из рисунка, следящая система содержит безинерционное звено с коэффициентом усиления «К», два интегрирующих звена, два форсирующих звена и два инерционных.

3. Передаточная функция и дифференциальное уравнение замкнутой системы.

Передаточная функция замкнутой системы дана в задании.

(6)

Преобразуем передаточную функцию к следующему виду и запишем дифференциальное уравнение.

	(7)
Для получения дифференциального уравнения необходимо найти его коэффициенты. Как известно коэффициенты дифференциального уравнения и коэффициенты передаточной функции замкнутой системы это одно и тоже. Поэтому подставим конкретные значения в выражение Ф(p):
	(8)
Отсюда согласно [4] дифференциальное уравнение замкнутой системы
	(9)

4. Передаточная функция для ошибки от возмущающего воздействия.

Передаточная функция ошибки записывается через передаточную функцию разомкнутой системы ( см. [4] ), или как отношение двух характеристических полиномов – разомкнутой системы А(р) и замкнутой – G(p).

	(10)
К(р)=В(р)/А(р); Ф(p)=B(p)/G(p))	(11)
А(р) это согласно (11) знаменатель уже найденной передаточной функции разомкнутой системы,  G(p) – знаменатель так же известной передаточной функции замкнутой системы. И в результате, подставив в формулу передаточной функции ошибки  вместо числителя характеристический полином разомкнутой системы А(р), а вместо знаменателя – характеристический полином замкнутой системы G(p), получим:
		(12)

5. Характеристический полином разомкнутой системы и вычисление его коэффициентов.

А(р) – характеристический полином разомкнутой системы. Как видно из (13) характеристический полином разомкнутой системы является знаменателем К(р). Запишем К(р). Из [4]

(13)

Используя формулу (4) запишем этот полином в виде

(14)

Найдем коэффициенты.

	(15)
	(16)
	(17)
	(18)
	(19)