Министерство образования и науки Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра РПиРПУ
Расчетно-графическое задание №1
Вариант 46
Факультет: РЭФ
Группа: РТВ 14-81
Студент: Лукинских Ю.А.
Преподаватель: Лявданский С.Е.
Дата:
Новосибирск 2011
Исходные данные
Структура системы: 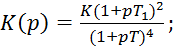
|
K |
T, c |
T1, c |
T2, c |
T3, c |
A |
B, 1/c |
C, 1/c2 |
D, 1/c3 |
|
15 |
0.03 |
1 |
0.3 |
0.09 |
0.4 |
0.6 |
-1.2 |
0.25 |
Задание на работу
1. По имеющейся в исходных данных передаточной функции разомкнутой системы записать передаточную функцию замкнутой системы
Передаточная функция
разомкнутой системы: 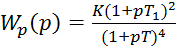
Передаточная
функция замкнутой системы: 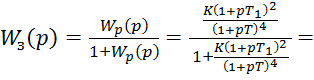
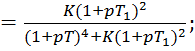
2. Записать передаточную функцию для ошибки от регулирующего воздействия.
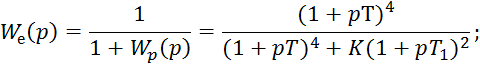
3. Изобразить структурную схему исследуемой системы, считая систему следящей.
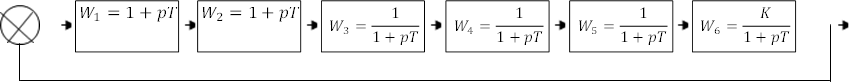 |
Рис.1 Структурная схема исследуемой системы
4. Записать характеристические полиномы разомкнутой и замкнутой системы.
Зная передаточную функцию разомкнутой системы, мы можем получить характеристический полином разомкнутой системы A(p):
![]()
Зная передаточную функцию замкнутой системы, мы можем получить характеристический полином замкнутой системы G(p):
![]()
![]()
5. Исследовать систему на устойчивость по критерию Гурвица.
Из предыдущего пункта возьмем характеристический полином замкнутой системы:
![]()
![]()
Коэффициенты характеристического полинома:
![]()
![]()
Необходимое условие выполняется.
Достаточное условие:
матрица Гурвица 
![]()
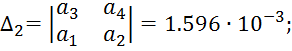
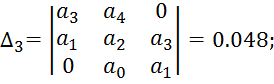
 Мы видим что все
диагональные определители >0 а следовательно достаточное условие
выполняется.
Мы видим что все
диагональные определители >0 а следовательно достаточное условие
выполняется.
Условие Гурвица для системы 4-го порядка:
![]()
После подстановки коэффициентов получаем:
![]()
Теперь найдем критический коэффициент усиления ККР для этого неравенство превратим в равенство:
![]()
Корни данного уравнения:
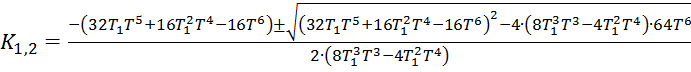
Откуда ![]()
![]()
6. Исследовать систему на устойчивость по критерию Михайлова методом чередующихся корней.
Характеристический полином нашей системы имеет вид:
![]()
![]()
Перейдем в частотную область:
![]()
Обозначим и вычислим коэффициенты:
![]()
![]()
![]()
![]()
![]()
Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.
![]() пусть
пусть ![]() , тогда
, тогда
![]()
![]()
![]()
Отсюда получаем: ![]()
![]()
Находим частоты пересечения вещественной оси:
![]()
![]()
![]()
Расположим частоты пересечения осей по порядку их возрастания, корни вещественной части подчеркнем одной чертой, корни мнимой двумя:
![]()
![]()
![]()
![]()
Корни чередуются, правило чередующихся корней выполняется, а следовательно система устойчива.
7. Построить годограф Михайлова с указанием масштабов по обеим осям.
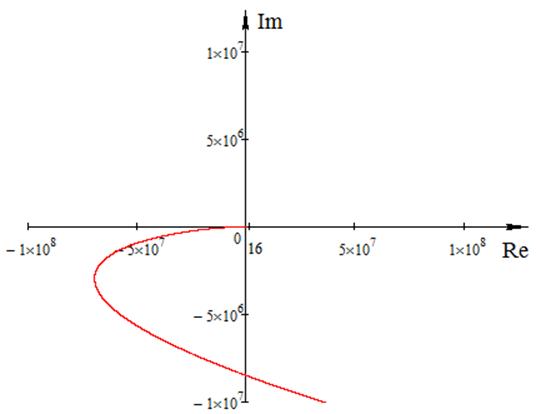
Рис.2 Годограф Михайлова
Корни чередуются. Правило чередующихся коней выполнятся, следовательно, система устойчива. Можно нарисовать, как выглядит годограф Михайлова.
8. Исследовать систему на устойчивость по критерию Найквиста.
Система РА, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если годограф частотной характеристики разомкнутой системы не охватывает точку с координатами (-1, j0). В том случае, когда годограф частотной характеристики охватывает эту точку, система неустойчива.
Запишем частотную
характеристику разомкнутой цепи: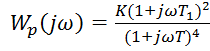
Изменение частоты
возьмем с от 0 до 200, с шагом 0.02: ![]()
9. Построить годограф Найквиста с указанием масштабов по обеим осям.
Годограф Найквиста будет иметь вид:
 Как мы видим годограф
Найквиста не охватывает точку с координатами (-1,j0) а следовательно система
устойчива.
Как мы видим годограф
Найквиста не охватывает точку с координатами (-1,j0) а следовательно система
устойчива.
Рис.3 Годограф Найквиста
10. Определить запас устойчивости по модулю и по фазе.
Как видно из рис.3
годограф пересекает ось Х на частоте ![]()
Запас по устойчивости по модулю равен расстоянию между точной (15, j0) и точкой
(-1, 0), отсюда ![]()
Запас устойчивости по фазе 180-arg(K(wкр)), где wкр это частота на которой
![]() ,
она равна 4.3 кГц, отсюда запас устойчивости равен 0.027
,
она равна 4.3 кГц, отсюда запас устойчивости равен 0.027
11. Вычислить
коэффициенты ошибки и найти ошибку регулирования системы в установившемся
режиме ![]() при заданной входной функции.
при заданной входной функции.
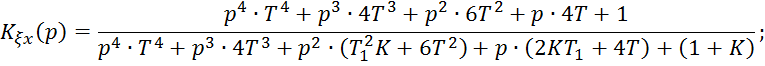
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Найдем коэффициенты ошибки:
![]()
![]()
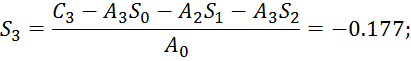
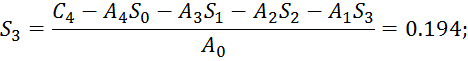
![]()
![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.