Устойчивость линейных систем и коррекция

Министерство образования и науки Российской Федерации

Новосибирский государственный технический университет

Кафедра РП и РПУ

Лабораторная работа №2 по курсу

«Радиоавтоматика».

Тема: Устойчивость линейных систем и коррекция.

Факультет: РЭФ

Группа: РТВ14-92

Студент: Шатров М.С.

Преподаватель: Лявданский С.Е.

Новосибирск 2012

Цель работы: исследовать устойчивости двух различных линейных систем автоматического регулирования, а также влияние на устойчивость и запас устойчивости системы введенных в ее структуру различных корректирующих звеньев.  

Структурные схемы систем №1 и №2.

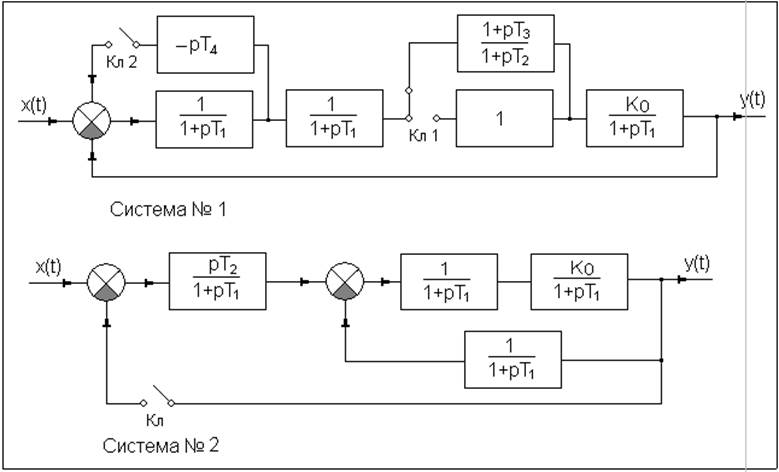
Ход работы:

1.1. Исследуется устойчивость системы №1 без коррекции. Система №1 без коррекции содержит в своём составе три инерционных звена с одинаковыми постоянными времени ; при этом звено последовательной коррекции (упругое дифференцирующее) и звено параллельной коррекции (идеальное дифференцирующее) отключены. Коэффициент усиления системы выбран таким, чтобы без коррекции система была неустойчива:

                          

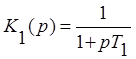
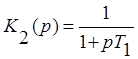
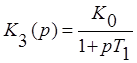
Передаточная функция разомкнутой системы без коррекции:

 

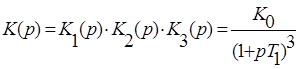
Запишем аналитическое выражение, по которому строится годограф Найквиста:

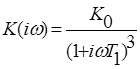
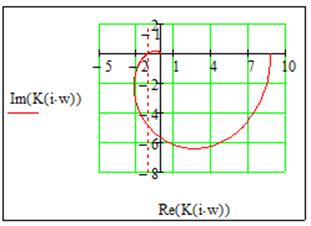
Передаточная функция замкнутой системы без коррекции:

 .

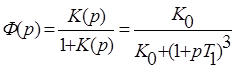Запишем характеристический полином, по которому строится годограф Михайлова:

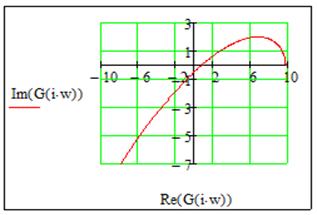
Вывод

По годографу Найквиста и Михайлова видно, что система не устойчива, т.к. годограф Найквиста охватывает на вещественной оси -1, а годограф Михайлова перепрыгивает из I квадранта в IV, а затем в III.

1.2. Подключается упругое дифференцирующее звено последовательной коррекции (именно такое состояние ключа Кл1 показано на схеме системы №1). Видно, что система стала устойчивой:

             

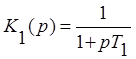
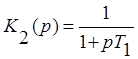
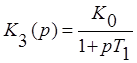
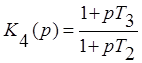
Передаточная функция разомкнутой системы с последовательной коррекцией:

 

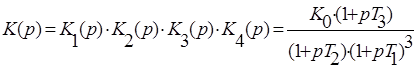
Запишем аналитическое выражение, по которому строится годограф Найквиста:

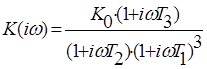
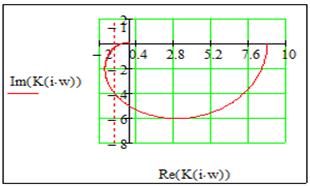
Передаточная функция замкнутой системы с последовательной коррекцией:

 .

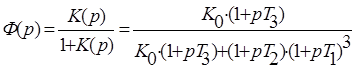Запишем характеристический полином, по которому строится годограф Михайлова:

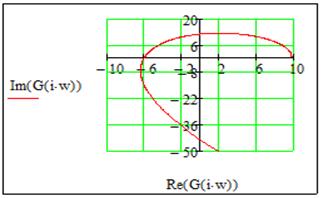
Вывод

По годографу Найквиста и Михайлова видно, что система устойчива, т.к. годограф Найквиста не охватывает на вещественной оси -1, а годограф Михайлова проходит против часовой стрелки по порядку из I квадранта во II, потом в III и IV квадрант. Кроме того можно заметить, что эффективность системы с последовательной коррекцией увеличилась по сравнению с системой без коррекции.

1.3. Отключается упругое дифференцирующее звено последовательной коррекции и подключается звено параллельной коррекции. Система снова устойчива, но видно, что эффективность коррекции явно увеличилась:

            

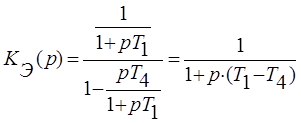
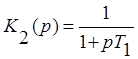
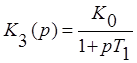
Передаточная функция разомкнутой системы с параллельной коррекцией:

 

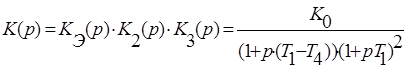
Запишем аналитическое выражение, по которому строится годограф Найквиста:

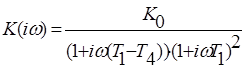
Передаточная функция замкнутой системы с параллельной коррекцией:

 .

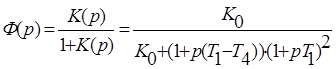Запишем характеристический полином, по которому строится годограф Михайлова:

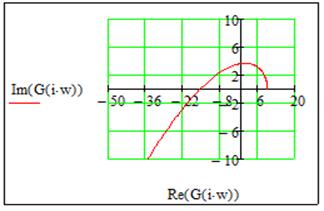
Вывод

По годографу Найквиста и Михайлова видно, что система устойчива, т.к. годограф Найквиста не охватывает на вещественной оси -1, а годограф Михайлова проходит против часовой стрелки по порядку из I квадранта во II, а затем в III. Кроме того можно заметить, что увеличился запас устойчивости  по сравнению с последовательной коррекцией.

1.4. Те же исследования проводятся для случая комбинированной коррекции, когда включены оба корректирующие звена. Эффективность коррекции ещё больше:

            

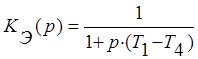
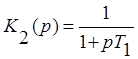
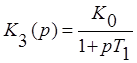
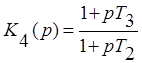
Передаточная функция разомкнутой системы с комбинированной коррекцией:

 

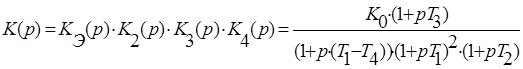
Запишем аналитическое выражение, по которому строится годограф Найквиста:

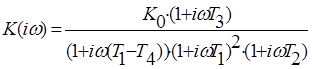
Передаточная функция замкнутой системы с комбинированной коррекцией:

 .

Запишем характеристический полином, по которому строится годограф Михайлова:

Вывод

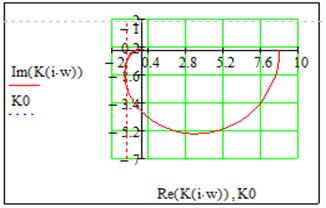
По годографу Найквиста и Михайлова видно, что система устойчива, т.к. годограф Найквиста не охватывает на вещественной оси -1, а годограф Михайлова проходит против часовой стрелки по порядку из I квадранта во II, потом в III и IV квадрант. Кроме того можно заметить, что запас устойчивости очень большой по сравнению с последовательной и параллельной коррекцией.

2. Исследуется система №2. Отличительной особенностью этой системы является два канала обратной связи: на главный (внешний) сумматор, и на внутренний сумматор. Эта система в данной лабораторной работе предназначена для конкретной иллюстрации того случая, когда разомкнутая система может быть неустойчивой (ключ в обратной связи разомкнут), а замкнутая система оказывается устойчивой:

    

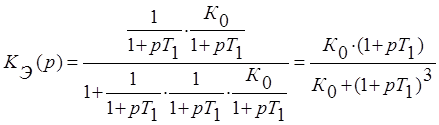
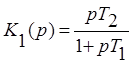
Передаточная функция разомкнутой  и замкнутой системы:

                                       

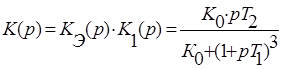
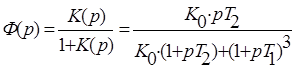
Запишем аналитические выражения, по которым строятся годографы Найквиста и Михайлова:

                                                                      

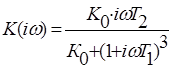
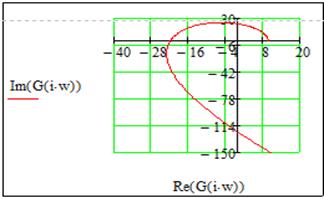
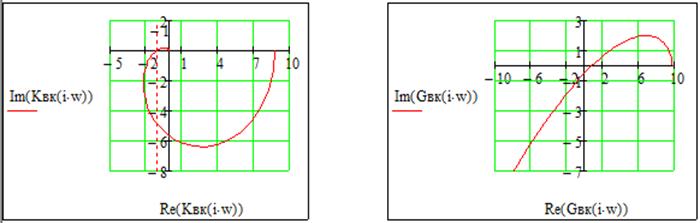
Годографы Найквиста и Михайлова для разомкнутой системы:

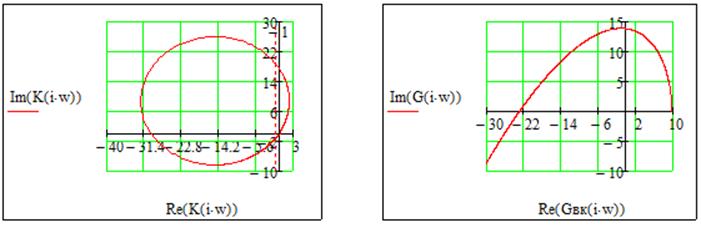
Годографы Найквиста и Михайлова для замкнутой системы:

Вывод

По годографу Найквиста и Михайлова видно, что разомкнутая система неустойчива, т.к. годограф Найквиста охватывает на вещественной оси -1, а годограф Михайлова перепрыгивает из I квадранта в IV, а затем в III.

По годографу Найквиста и Михайлова видно, что замкнутая система устойчива, т.к. годограф Найквиста против часовой стрелки охватывает на вещественной оси точку -1 m/2 раз, а годограф Михайлова проходит против часовой стрелки по порядку из I квадранта во II, а затем в III.