Исследование свойств нелинейных систем (устойчивости и формы импульсной характеристики)

      Цель работы: исследование свойств нелинейных систем (устойчивости и формы импульсной характеристики). В работе исследуются несколько структур нелинейных систем, а именно:

- два варианта линейной части системы: статическая из трёх инерционных звеньев, а также астатическая из одного интегрирующего и двух инерционных звеньев;

- три варианта нелинейностей с каждой из вышеупомянутых линейных частей: нелинейности «насыщение», «зона нечувствительности», «зона нечувствительности с насыщением».

Выполнение работы.

1.  Система с нелинейностью «насыщение».

Характеристика нелинейного элемента задается функцией:

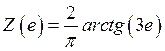                                                                (1.1)

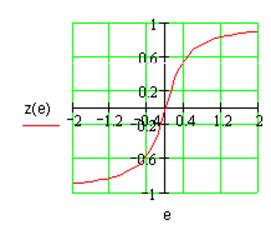
                                             Рис. 1.1. Характеристика системы с нелинейностью «насыщение».

1.1.   Линейная часть – статическая устойчивая система.

Передаточная функция линейной части:

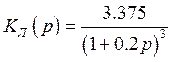                                                           (1.2)

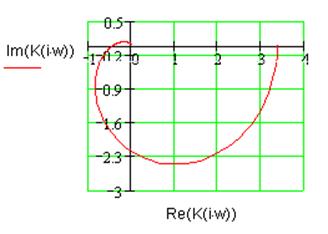
                                                      Рис. 1.2. Годограф Найквиста линейной части .

Как видно из рис. 1.2, годограф Найквиста не охватывает точку -1 вещественной оси комплексной плоскости, что означает устойчивость линейной части нелинейной системы.

Характеристиками устойчивости нелинейной системы являются диаграмма Гольдфарба и фазовый портрет системы.

  а) Диаграмма Гольдфарба                                               б) Фазовый портрет              

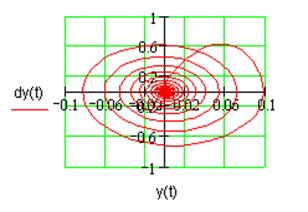
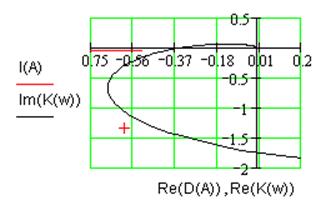
Рис. 1.3. Характеристики устойчивости нелинейной системы.

При построении диаграммы Гольдфарба на одной координатной системе комплексной плоскости строится годограф комплексного коэффициента передачи линейной части системы как функция частоты , а также годограф функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды 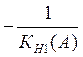. На рис. 1.2а видно, что указанные годографы не пересекаются, а это, согласно методу Гольдфарба, означает устойчивость нелинейной системы.   

Фазовый портрет нелинейной системы строится на так называемой фазовой плоскости, где по горизонтали откладывается величина исследуемой функции (обычно выход системы), а по вертикали – её первая производная. Если в системе возможны устойчивые автоколебания, то фазовая траектория, двигаясь по часовой стрелке, асимптотически приближается к замкнутой кривой (часто эллипс), называемой предельным устойчивым циклом, и будет вращаться там до выключения системы. Если же в системе невозможны автоколебания, фазовый портрет представляет собой спираль, сходящуюся в состояние покоя системы (часто начало координат). На рис. 1.2б видно, что все фазовые траектории сходятся в точку устойчивого равновесия (начало координат), что подтверждает вывод об устойчивости данной нелинейной системы.

1.2.  Линейная часть – статическая неустойчивая система.

Передаточная функция линейной части:

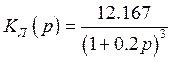                                                           (1.3)

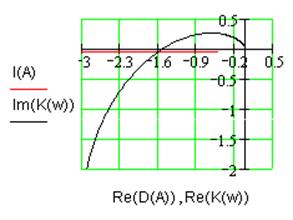
                                                        Рис. 1.4. Диаграмма Гольдфарба нелинейной  системы.

Как видно из рис. 1.4, увеличение коэффициента усиления линейной части системы привело к пересечению годографов на диаграмме Гольдфарба. Это означает, что в системе возможны автоколебания. При этом согласно методу Гольдфарба эти автоколебания будут устойчивы в точке пересечения годографов, если при приращении аргумента А на годографе нелинейной части он выходит из пределов комплексной плоскости, очерченных годографом линейной части. Если же годограф нелинейной части входит внутрь вышеуказанной области комплексной плоскости, то автоколебания будут неустойчивыми, то есть, практически их нельзя будет наблюдать. В данном случае годограф нелинейной части выходит из области, очерченной годографом линейной части, что означает наличие устойчивых автоколебаний на частоте   с амплитудой .

Устойчивость возникающих в системе автоколебаний подтверждается импульсной характеристикой системы (рис. 1.5), имеющей вид незатухающих автоколебаний:

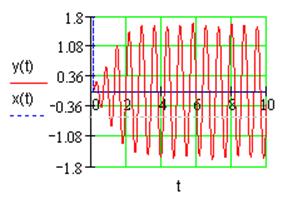
                                                              Рис. 1.5. Импульсная характеристика системы.

1.3.  Линейная часть – астатическая устойчивая система.

Передаточная функция линейной части:

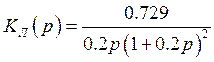                                                           (1.4)

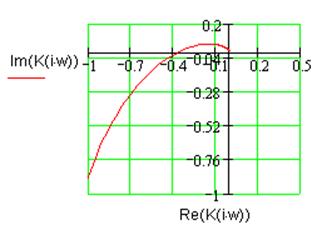
                                                    Рис. 1.6. Годограф Найквиста линейной части .

Годограф Найквиста линейной части системы не охватывает точку -1 (см. рис. 1.6), следовательно, линейная часть системы устойчива. 

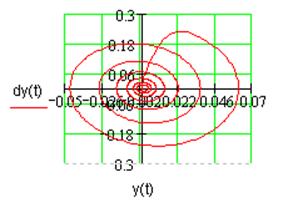
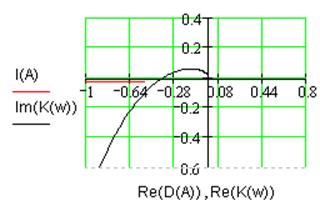
а) Диаграмма Гольдфарба                                        б) Фазовый портрет              

Рис. 1.7. Характеристики устойчивости нелинейной системы.

Как видно из рис. 1.7а,  годографы  и 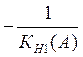 не пересекаются, что означает невозможность возникновения автоколебаний в системе. На фазовом портрете системы (рис. 1.7б) в этом случае все фазовые траектории сходятся в точку устойчивого равновесия.

1.4.  Линейная часть – астатическая неустойчивая система.

Передаточная функция линейной части:

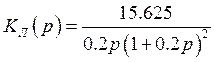                                                           (1.5)

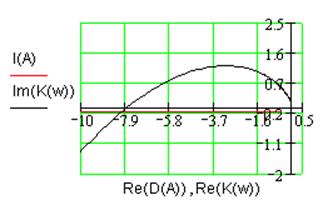
                                       Рис. 1.8. Диаграмма Гольдфарба нелинейной  системы.

Увеличение коэффициента усиления линейной части системы привело к пересечению годографов  и 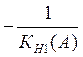 (см. рис. 1.8). Причем это пересечение таково, что годограф нелинейной части выходит из области, очерченной годографом линейной части, что означает наличие устойчивых автоколебаний на частоте   с амплитудой .

Устойчивость возникающих в системе автоколебаний подтверждается импульсной характеристикой системы (рис. 1.9), имеющей вид незатухающих автоколебаний: