Исследование свойств нелинейных систем (устойчивости и формы импульсной характеристики), страница 2

                                                         Рис. 1.9. Импульсная характеристика системы.

2.  Система с нелинейностью «зона нечувствительности».

Характеристика нелинейного элемента задается функцией:

                                                                (2.1)

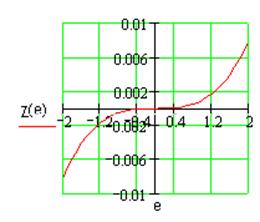
                                 Рис. 2.1. Характеристика системы с нелинейностью «зона нечувствительности».

2.1.  Линейная часть – статическая устойчивая система.

Передаточная функция линейной части:

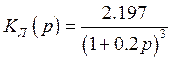                                                           (2.2)

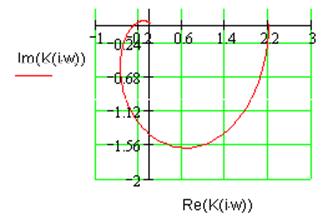
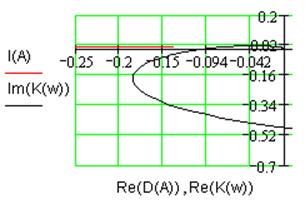
                                                     Рис. 2.2. Годограф Найквиста линейной части .

Годограф Найквиста линейной части системы не охватывает точку -1 (см. рис. 2.2), следовательно, линейная часть системы устойчива. 

а) Диаграмма Гольдфарба                                                б) Фазовый портрет              

Рис. 2.3. Характеристики устойчивости нелинейной системы.

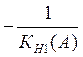Как видно из рис. 2.3а,  годографы  и  не пересекаются, что означает невозможность возникновения автоколебаний в системе. На фазовом портрете системы (рис. 2.3б) в этом случае все фазовые траектории сходятся в точку устойчивого равновесия.

2.2.  Линейная часть – статическая неустойчивая система.

Передаточная функция линейной части:

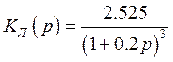                                                           (2.3)

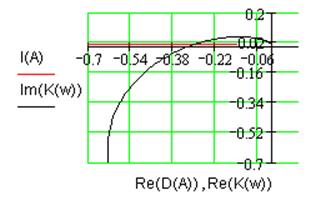
                                                   Рис. 2.4. Диаграмма Гольдфарба нелинейной  системы.

Увеличение коэффициента усиления линейной части системы привело к пересечению годографов  и 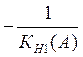 (см. рис. 2.4). Причем это пересечение таково, что годограф нелинейной части выходит из области, очерченной годографом линейной части, что означает наличие устойчивых автоколебаний на частоте   с амплитудой .

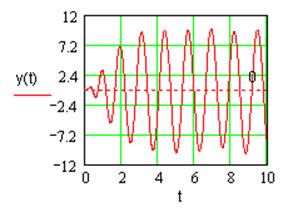
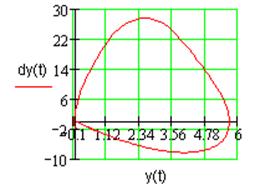
Устойчивость возникающих в системе автоколебаний подтверждается импульсной характеристикой системы (рис. 2.5), имеющей вид незатухающих автоколебаний:

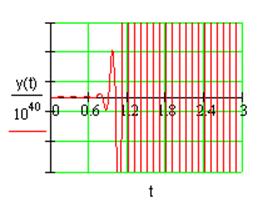
                                                              Рис. 2.5. Импульсная характеристика системы.

2.3.  Линейная часть – астатическая устойчивая система.

Передаточная функция линейной части:

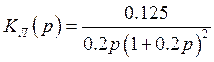                                                           (2.4)

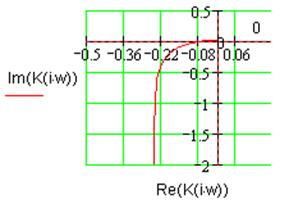
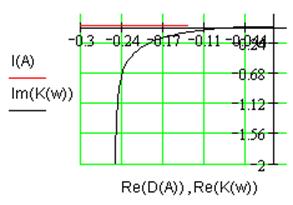
                                                              Рис. 2.6. Годограф Найквиста линейной части .

Годограф Найквиста линейной части системы не охватывает точку -1 (см. рис. 2.6), следовательно, линейная часть системы устойчива. 

         а) Диаграмма Гольдфарба                                                б) Фазовый портрет              

Рис. 2.7. Характеристики устойчивости нелинейной системы.

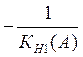Как видно из рис. 2.7а,  годографы  и  не пересекаются, что означает невозможность возникновения автоколебаний в системе. На фазовом портрете системы (рис. 2.7б) в этом случае все фазовые траектории сходятся в точку устойчивого равновесия.

2.4.  Линейная часть – астатическая неустойчивая система.

Передаточная функция линейной части:

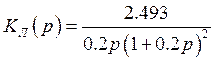                                                           (2.5)

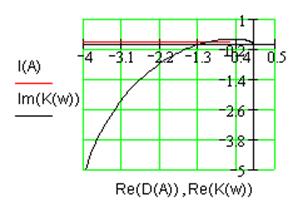
                                                 Рис. 2.8. Диаграмма Гольдфарба нелинейной  системы.

Увеличение коэффициента усиления линейной части системы привело к пересечению годографов  и 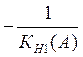 (см. рис. 2.8). Причем это пересечение таково, что годограф нелинейной части выходит из области, очерченной годографом линейной части, что означает наличие устойчивых автоколебаний на частоте   с амплитудой .

Устойчивость возникающих в системе автоколебаний подтверждается импульсной характеристикой системы (рис. 2.9), имеющей вид незатухающих автоколебаний:

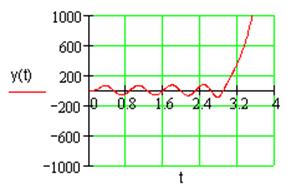
                                                            Рис. 2.9. Импульсная характеристика системы.

3.  Система с нелинейностью «зона нечувствительности с насыщением».

Характеристика нелинейного элемента задается функцией:

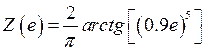                                                                (3.1)

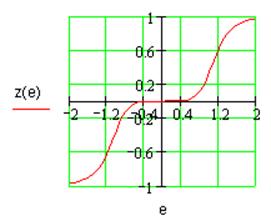
Рис. 3.1. Характеристика системы с нелинейностью «зона нечувствительности с  насыщением».

3.1.  Линейная часть – статическая устойчивая система.

Передаточная функция линейной части:

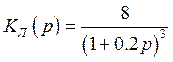                                                           (3.2)

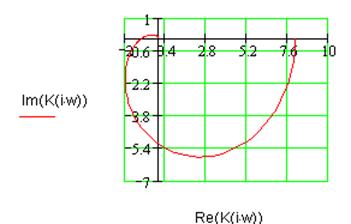
Рис. 3.2. Годограф Найквиста линейной части .

Годограф Найквиста линейной части системы не охватывает точку -1 (см. рис. 3.2), следовательно, линейная часть системы устойчива.

        

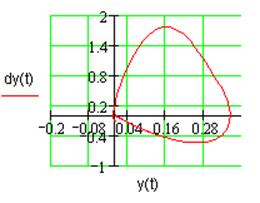
а) Диаграмма Гольдфарба                                          б) Фазовый портрет              

Рис. 3.3. Характеристики устойчивости нелинейной системы.

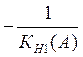Как видно из рис. 3.3а,  годографы  и  не пересекаются, что означает невозможность возникновения автоколебаний в системе. На фазовом портрете системы (рис. 3.3б) в этом случае все фазовые траектории сходятся в точку устойчивого равновесия.

3.2.  Линейная часть – статическая неустойчивая система.

Передаточная функция линейной части:

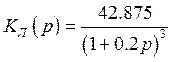                                                           (3.3)

   

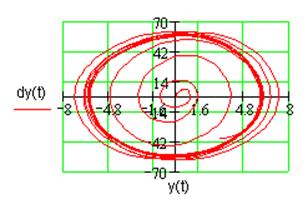
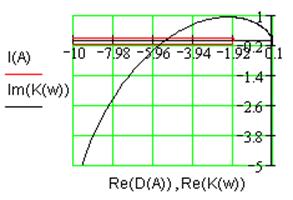
а) Диаграмма Гольдфарба                                               б) Фазовый портрет              

Рис. 3.4. Характеристики устойчивости нелинейной системы.

Увеличение коэффициента усиления линейной части системы привело к пересечению годографов  и 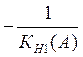 (см. рис. 3.4а). Причем это пересечение таково, что годограф нелинейной части выходит из области, очерченной годографом линейной части, что означает наличие устойчивых автоколебаний на частоте   с амплитудой .

Точке пересечения годографов на диаграмме Гольдфарба соответствует замкнутый предельный цикл на фазовом портрете (рис. 3.4б).