Исследование устойчивости двух различных линейных систем автоматического регулирования

Цель работы: исследование устойчивости двух различных линейных систем автоматического регулирования, а также влияние на устойчивость и запас устойчивости системы введенных в её структуру различных корректирующих звеньев.

1. Исследование устойчивости системы №1.

1.1. Система №1 без коррекции

                                                Рис.1.1 Структурная схема системы №1без коррекции

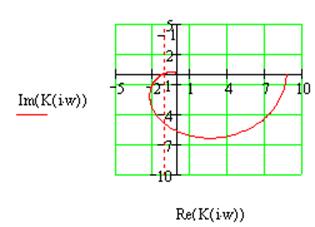
                                               Рис.1.2 Годограф Найквиста для системы №1 без коррекции

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста:

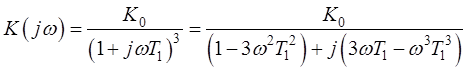
Как видно из рис. 1.2, годограф Найквиста охватывает точку -1 на вещественной оси, следовательно, данная система неустойчива.

  

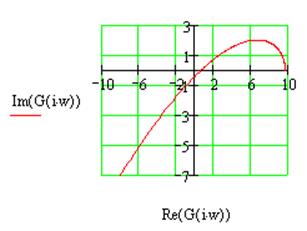
Рис.1.3 Годограф Михайлова для системы №1 без коррекции

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

Как видно из рис. 1.3, годограф Михайлова проходит квадранты на комплексной плоскости не последовательно, поэтому данная система неустойчива.

Неустойчивость системы №1 без коррекции подтверждается переходной характеристикой:

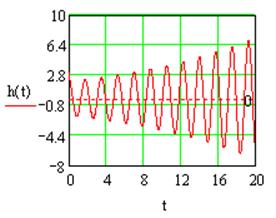
Рис.1.4 Переходная характеристика системы №1 без коррекции

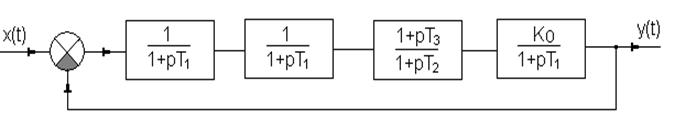1.2. Система №1 с последовательной коррекцией.

                                        Рис.1.5 Структурная схема системы №1с последовательной коррекцией

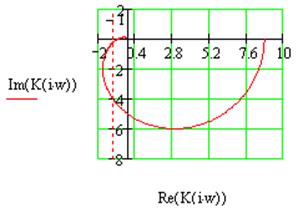
                                      Рис.1.6 Годограф Найквиста для системы №1с последовательной коррекцией

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста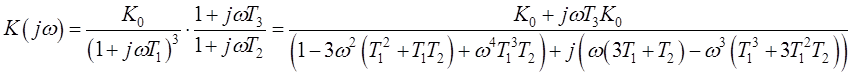

Как видно из рис. 1.6, годограф Найквиста  не охватывает точку -1 на вещественной оси, следовательно, данная система устойчива.

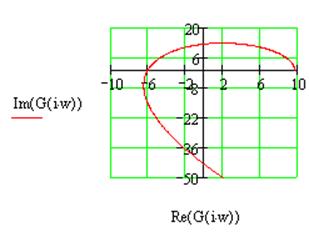
                                  Рис.1.7 Годограф Михайлова для системы №1с последовательной коррекцией

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

Как видно из рис. 1.7, годограф Михайлова проходит последовательно против часовой стрелки четыре квадранта на комплексной плоскости, что согласно критерию Михайлова означает устойчивость данной системы.

Устойчивость системы №1 с последовательной коррекцией подтверждается переходной характеристикой:

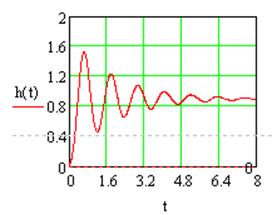
Рис.1.8 Переходная характеристика системы №1с последовательной коррекцией

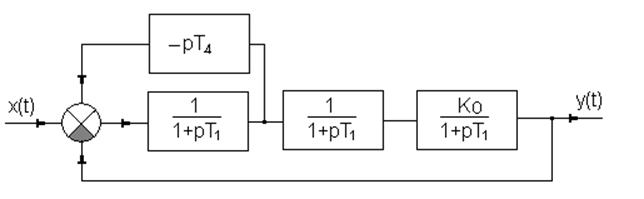
1.3. Система №1 с параллельной коррекцией.

                      Рис.1.9 Структурная схема системы №1с последовательной коррекцией

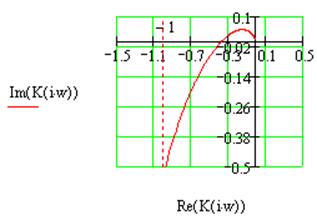
                          Рис.1.10 Годограф Найквиста для системы №1с параллельной коррекцией

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста

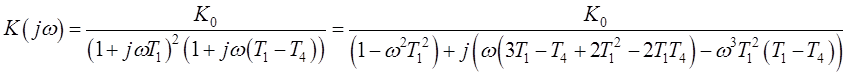
Как видно из рис. 1.10, годограф Найквиста  не охватывает точку -1 на вещественной оси, следовательно, данная система устойчива. Кроме того, из сравнения рисунков 1.10 и 1.6 можно сделать вывод о том применение параллельной коррекции позволяет увеличить запас устойчивости, как по фазе, так и по амплитуде.  

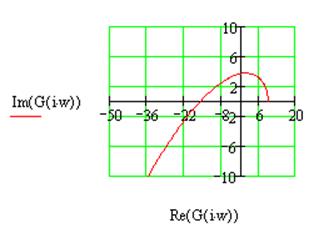
                                Рис.1.11 Годограф Михайлова для системы №1с параллельной коррекцией

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

Как видно из рис. 1.11, годограф Михайлова проходит последовательно против часовой стрелки три квадранта на комплексной плоскости, что согласно критерию Михайлова означает устойчивость данной системы.

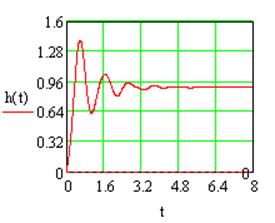Устойчивость системы №1 с параллельной коррекцией подтверждается переходной характеристикой:

Рис.1.12 Переходная характеристика системы №1с параллельной коррекцией

1.4. Система №1 с комбинированной коррекцией.

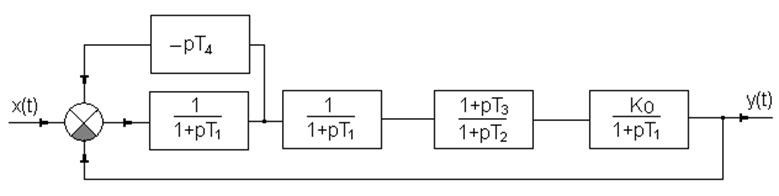
                                   Рис.1.13 Структурная схема системы №1скомбинированной коррекцией

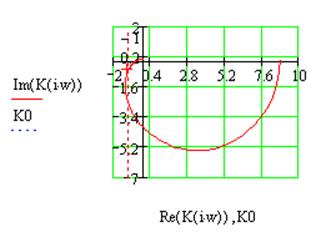
                          Рис.1.14 Годограф Найквиста для системы №1с комбинированной коррекцией

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста

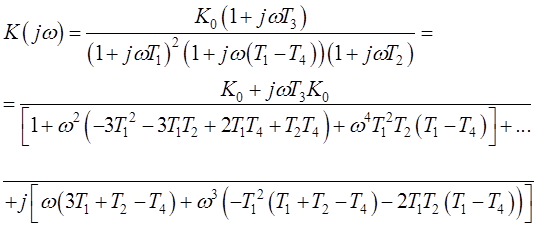
Как видно из рис. 1.14, годограф Найквиста  не охватывает точку -1 на вещественной оси, следовательно, данная система устойчива. Кроме того комбинированная коррекция обеспечивает больший запас устойчивости по амплитуде и по фазе чем при параллельной и последовательной коррекции.

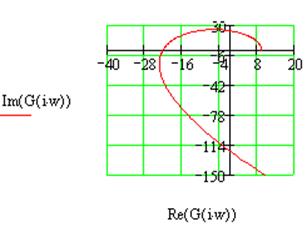
                                Рис.1.15 Годограф Михайлова для системы №1с комбинированной коррекцией

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

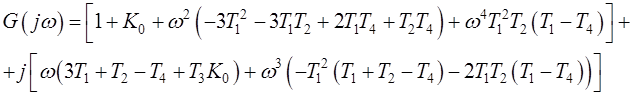
Как видно из рис. 1.15, годограф Михайлова проходит последовательно против часовой стрелки четыре квадранта на комплексной плоскости, что согласно критерию Михайлова означает устойчивость данной системы.

Устойчивость системы №1 с комбинированной коррекцией подтверждается переходной характеристикой:

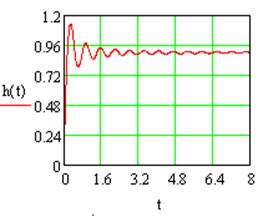
Рис.1.16 Переходная характеристика системы №1с комбинированной коррекцией

2. Исследование устойчивости системы №2.

2.1. Система №2 в разомкнутом состоянии

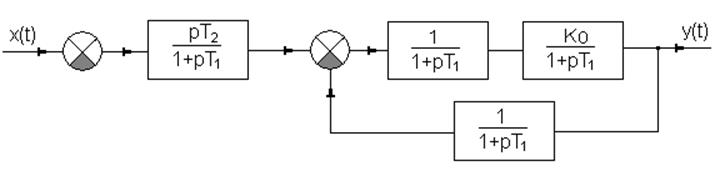
                                   Рис.2.1 Структурная схема системы №2 в разомкнутом состоянии.

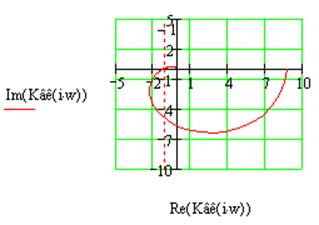
                                  Рис.2.2 Годограф Найквиста для системы №2 в разомкнутом состоянии.

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста

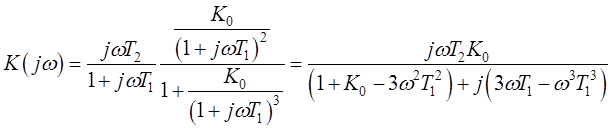
Как видно из рис. 2.2., годограф Найквиста охватывает точку -1 на вещественной оси комплексной плоскости, следовательно, данная система неустойчива.

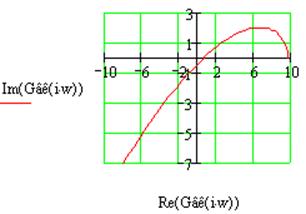
                                        Рис.2.3 Годограф Михайлова для системы №2 в разомкнутом состоянии.

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

Как видно из рис. 2.3., годограф Михайлова проходит квадранты на комплексной плоскости не последовательно, значит, данная система неустойчива.

Неустойчивость системы №2 в разомкнутом состоянии подтверждается переходной характеристикой:

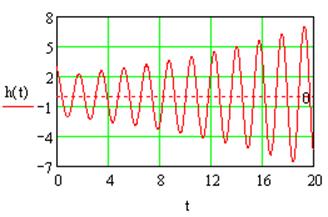
                           Рис.2.4 Переходная характеристика системы №2 в разомкнутом состоянии.

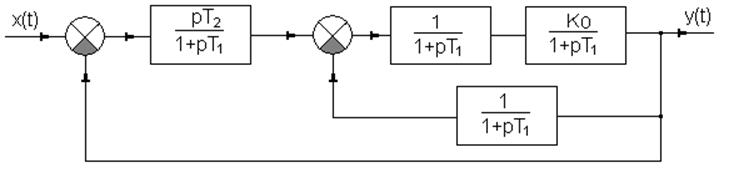2.2. Система №2 в замкнутом состоянии

                       Рис.2.5 Структурная схема системы №2 в замкнутом состоянии.

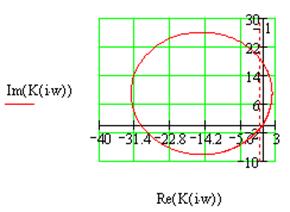
                                Рис.2.6 Годограф Найквиста для системы №2 в замкнутом состоянии.

Передаточная функция разомкнутой системы, по которой построен годограф Найквиста:

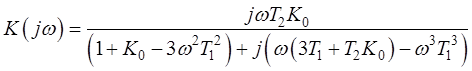
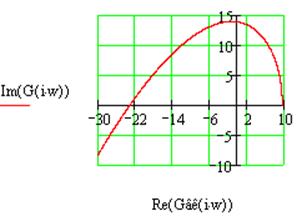
                                         Рис.2.7 Годограф Михайлова для системы №2 в замкнутом состоянии.

Характеристический полином замкнутой системы, по которому построен годограф Михайлова:

Поскольку годограф разомкнутой системы охватывает точку -1 вещественной оси комплексной плоскости 1 раз (количество корней с положительной  вещественной частью в характеристическом уравнении разомкнутой системы равно 2), причем против часовой стрелки, то данная система устойчива.

Устойчивость системы подтверждается переходной характеристикой:

 

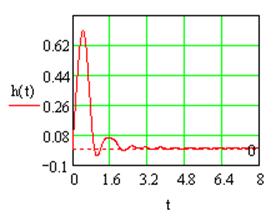
        Рис.2.8 Переходная характеристика системы №2 в замкнутом состоянии.

Замкнутую систему можно сделать неустойчивой, если изменить постоянную времени  дифференцирующего звена.

Годографы Найквиста и Михайлова, а также переходная характеристика, подтверждающие неустойчивость системы приведены ниже.

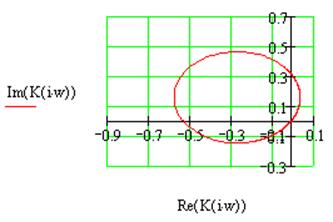
                                      Рис.2.9 Годограф Найквиста для системы №2 в замкнутом состоянии.

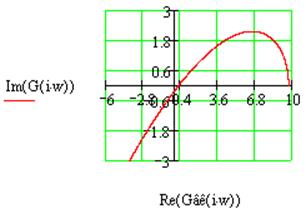
                                   Рис.2.10 Годограф Михайлова для системы №2 в замкнутом состоянии.

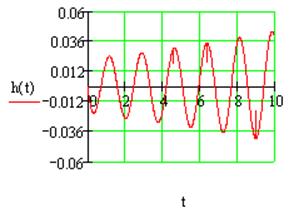
Рис.2.11 Переходная характеристика системы №2 в замкнутом состоянии.

В ходе лабораторной работе я убедился в полном соответствии полученных в процессе работы результатов с теорией.