В итоге, характеристический полином с найденными коэффициентами:
|
|
(20) |
6. Характеристический полином замкнутой системы и вычисление его коэффициентов.
По материалам [4] имеем:
|
|
(21) |
G(р) – характеристический полином замкнутой системы. Из формулы (8) получим этот полином:
|
|
(22) |
Найдем коэффициенты.
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
Характеристический полином с найденными коэффициентами:
|
|
(28) |
7. Анализ устойчивости системы по критерию Гурвица.
Проведем анализ устойчивости системы согласно [3]. Для этого необходимо из коэффициентов характеристического уравнения (22) составить матрицу Гурвица. С этой целью уравнение (22) запишем в виде
|
|
(29) |
Как видно из характеристического полинома, все коэффициенты положительны. Выполняется необходимое, но недостаточное условие устойчивости системы по алгебраическому критерию Гурвица. Проверим достаточное условие устойчивости – положительность всех диагональных определителей матрицы Гурвица. Составим матрицу nxn. При этом по главной диагонали с верхнего левого угла до нижнего правого запишем коэффициенты от (аn-1) до ао. Остальные места заполним так: по строке вправо вписываем коэффициенты с возрастанием индекса, влево – с убыванием.
|
|
(30) |
Если определитель матрицы (30) больше нуля, то система устойчива.
|
|
(30) |
|
|
(31) |
Определитель больше нуля, следовательно, система устойчива. И все корни уравнения (29) будут иметь отрицательные вещественные части.
8. Исследование устойчивости системы по критерию Михайлова (метод чередующихся корней). Построение годографа Михайлова.
Как
известно, по Михайлову система n – порядка будет устойчива, если годограф
характеристической частотной функции G(j![]() ) в диапазоне частот от нуля до
бесконечности последовательно против часовой стрелки обходит n квадратов
комплексной плоскости. Т.е. если система устойчива, то годограф функции G(j
) в диапазоне частот от нуля до
бесконечности последовательно против часовой стрелки обходит n квадратов
комплексной плоскости. Т.е. если система устойчива, то годограф функции G(j![]() ) поочередно пересекает вещественную и
мнимую оси и не может подряд два раза пересечь одну и ту же ось.
) поочередно пересекает вещественную и
мнимую оси и не может подряд два раза пересечь одну и ту же ось.
|
|
(32) |
Запишем G(p) как G(jw) и приравняем к нулю.
|
|
(33) |
|
|
(34) |
Найдем частоты пересечения с мнимой частью. Для этого вещественную часть приравняем нулю.
|
|
(35) |
Чтобы решить данное уравнение выполним замену переменной x = w2.
|
|
(36) |
|
|
(37) |
x1 = 1899,561 x2 = 0,439
w = 43,584/с w = 0,662 1/с
Теперь найдем частоты пересечения с вещественной частью. Для этого мнимую часть приравняем нулю.
|
|
(38) |
w = 0 1/с w = 15,811 1/с
Выстроим частоты по порядку и посмотрим, пересекаются ли где-нибудь оси два или более раз подряд.
0 0,662 15,881 43,584
Система устойчива, так как оси по порядку пересекаются не больше одного раза. Построим годограф Михайлова. Для этого найдем координаты пересечения годографа с осями.
w = 0 G(jw) = 80
w = 0,662 G(jw) = 108,601j
w = 15,881 G(jw) = -39820
w = 43,584 G(jw) = -69020j
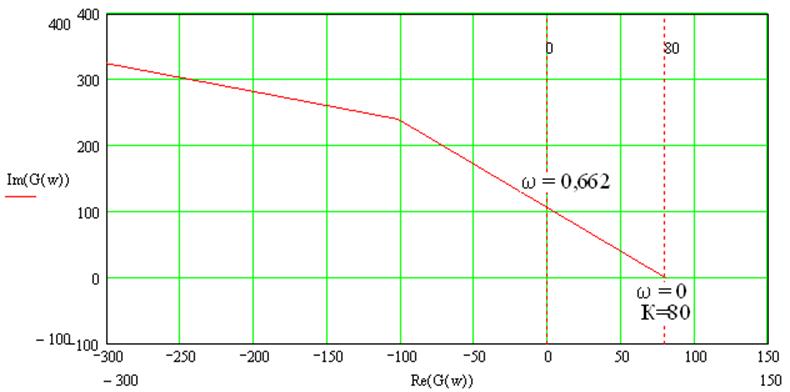
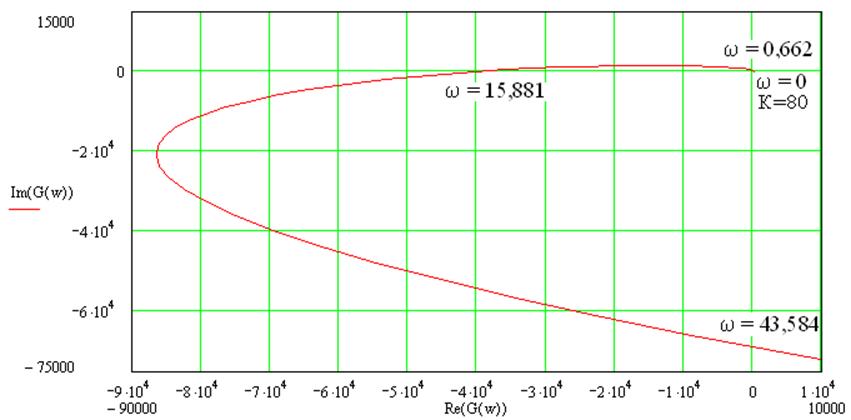 На рисунке 3, б показано в
более мелком масштабе, что годограф Михайлова не проходит через точку 0.
На рисунке 3, б показано в
более мелком масштабе, что годограф Михайлова не проходит через точку 0.
а)
 б)
б)
Рисунок 2. Годографы Михайлова в разном масштабе.
9. Исследование устойчивости системы по критерию Найквиста. Построение годографа Найквиста. Определение запаса устойчивости по модулю и по фазе.
Построим годограф К(р).
|
|
(39) |
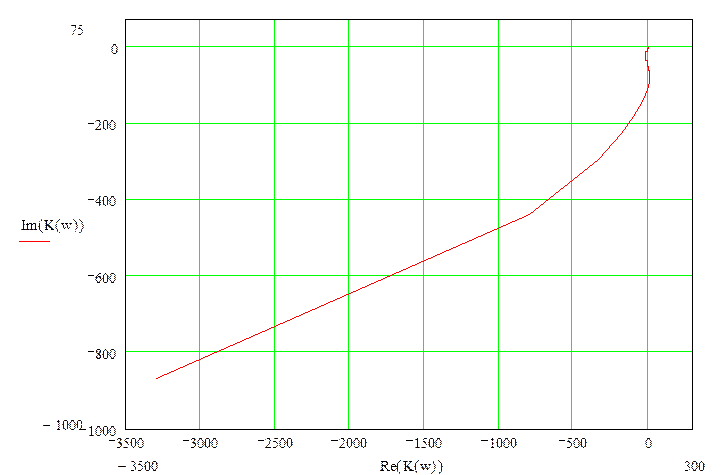
а)
б)
в)
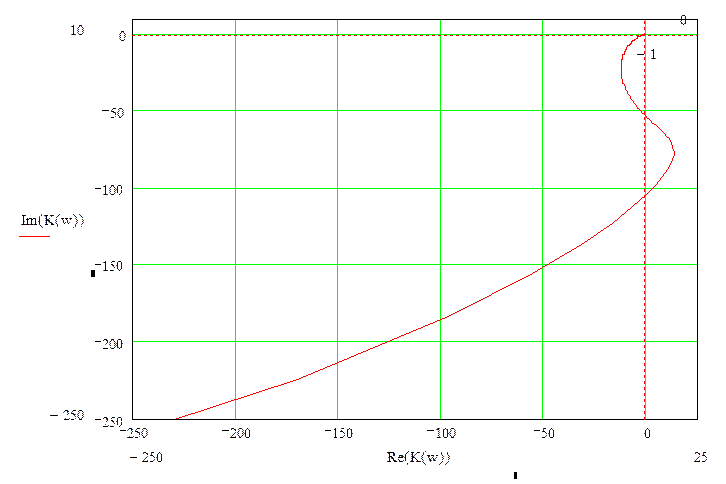
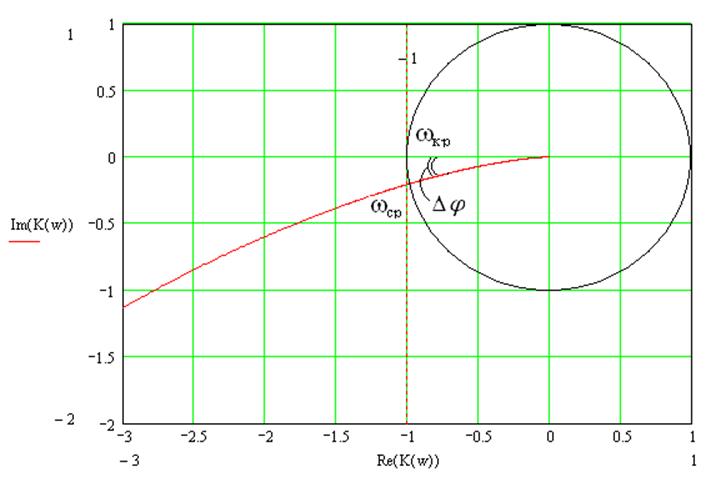
Рисунок 3. Годографы Найквиста в разном масштабе.
Годограф системы не охватывает точку «-1», следовательно, система устойчива.
Запасом устойчивости по амплитуде согласно [6] называют расстояние между критической точкой (-1, j0) и ближайшей к ней точкой пересечения АФХ с отрицательной полуосью абсцисс. Годограф Найквиста проходит через ноль, следователь запас устойчивости по модулю равен 1.
Запас устойчивости по фазе характеризует удаленность точки АФХ, соответствующей частоте среза от критической точки (-1,j0). Определим его в соответствии с рис. 3, как угол:
|
|
(40) |
10. Нахождение ошибки регулирования x(t) и построение графика.
Используем формулу для передаточной функции ошибки из материалов [4]:
|
|
(41) |
|
|
(42) |
|
|
(43) |
Рассчитаем коэффициенты Sn. Согласно [4] имеем:
|
|
(44) |
|
|
(45) |
|
|
(46) |
|
|
(47) |
|
|
(46) |
Зная коэффициенты, запишем дифференциальное уравнение ошибки.
|
|
(48) |
Зная возмущающее воздействие, найдем производные, подставим в уравнение ошибки и получим саму ошибку.
|
|
(49) |
|
|
(50) |
|
|
(51) |
|
|
(52) |
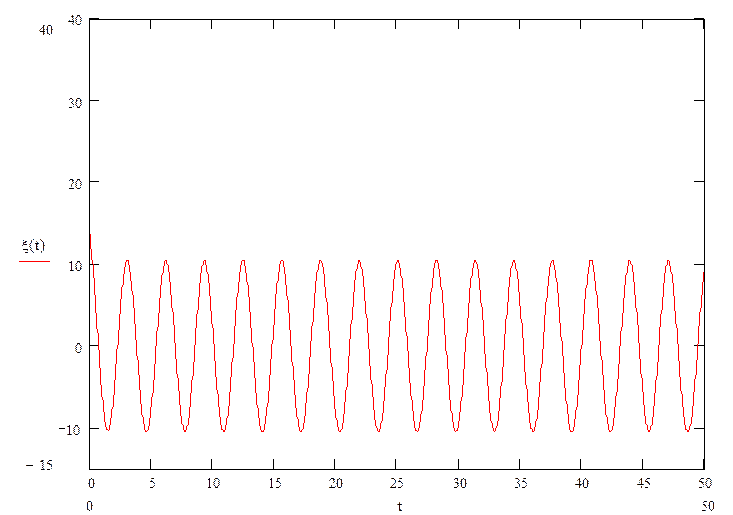
Рисунок 4. График ошибки регулирования.
Литература.
1. Коновалов Г.Ф. Радиоавтоматика–М.: В.Ш., 1990. – 335с.
2. Конспект лекций за 2004.
3. Лявданский С.Е. Методическое пособие Радиоавтоматика–Н.: НГТУ, 1990.–33с.
4. Лявданский С.Е. Методическое пособие Радиоавтоматика–Н.: НГТУ, 1995.–35с.
5. Первачев С.В. Радиоавтоматика–М.: Радио и связь, 1982. – 295с.
6. Радиоавтоматика / под редакцией Бессекерскрго –М.: В.Ш., 1985.–270с
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.