Радиотехническая система, страница 6

В частотной области связаны через коэффициент передачи.Моделирование РЭС в частотной области можно разделить на две группы: 1. Используя связь между частотными и частотными свойствами цепей. 2. Используя непосредственное моделирование параметров радиотехнических устройств. В ервой группе методы моделирования осуществляются с помощью прямого пеобразования Фурье, а затем рассчитывается спектр выходного сигнала по формуле:    

Для второй области используются следующие зависимости, притом частотные характеристики определяются непосредственно по параметрам цепи. Вторая группа моделирования более быстродействующая. Здесь возможен анализ устойчивости радиотехнического устройства. Первая группа более удобна при использовании матриц классической и волновой теории.

Применение  матриц в классической и волновой теории при моделировании РЭС

При частотном анализе все двух полюсные элементы, входящие в радиоэлектронную систему  характеризуются своим  реактивным сопротивлением, то есть  Z(jw) = r(w) + jX(w), или проводимостью Y(jw) = 1/Z(jw) = G(w) + jB(w)

Четырех полюсные и многополюсные элементы электронных схем описываются соответствующими матрицами параметров:

1. Соответствующие классической теории четырехполюсников.

2. Соответствующие волновой теории четырехполюсников.

Первая группа матриц: сопротивлении (Z), проводимостей(Y), прямой  передачи (А), гибридная (Н).

Вторая группа матриц: рассеяния (S), волновая матрица передачи (Т).

У данного четырехполюсника  фазовыми переменными, являются, которые полностью описывают данную цепь, являются частотные характеристики токов и напряжений на входе и выходе.Четырехполюсник соответствует теории матриц связывают две пары токов между соответствующими парами напряжений.. В этом случае есть две пары фазовых переменных, , а две зависимых от них. В зависимости от того какая пара  является фазовыми переменными  формируется та или иная матрица классической теории четырехполюсников. Возможно шесть комбинаций зависимых и независимых переменных.

Матрица сопротивлений (импендансов)

I₁, I₂ – независимы; U₁, U₂ – зависимы;

Z-параметры определяются в режиме холостого хода

Матрица Y-параметров (проводимости)                       

U₁, U₂ – независимы;

I₁, I₂ – зависимы;

y-параметры определяются в режиме КОРОТКОГО ЗАМЫКАНИЯ

Матрицы являются взаимообратными Y = Z^-1 => I = YU => Y^-1I = U => ZI = U

Матрица передачи или цепная матрица

Она соответствует передаче сигнала со входа на выход.

Следовательно независимыми фазовыми переменными являются выходные параметры четырехполюсника.

а₁₁ – коэффициент передачи по напряжению в режиме холостого хода по выходу.

а₁₂ – передаточной сопротивление в режиме короткого замыкания по выходу.

а₂₁ – передаточная проводимость в режиме холостого хода по выходу.

а₂₂ – коэффициент передачи по току в режиме короткого замыкания. по выходу.

Гибридная матрица  Н

Независимыми переменными считается ток I₁ и напряжение U₂

Большую схему можно разбить на отдельные четырехполюсники. Эти четырехполюсники, зная их характеристики находим соответствующие матрицы , а затем комбинируем данные четырехполюсники, можно получить требуемые характеристики всего устройства.

Матрица Z удобна при последовательном соединении четырехполюсников: Z = Σ(|Z_i|)

Матрица Y – при параллельном соединении четырехполюсников. Y = Σ (|Y_i|)

Цепная матрица удобна при каскадном соединении четырехполюсников. (Это когда ток и напряжение совпадает). А = П(|A_i|)

Гибридная матрица используется для макромоделирования транзистора, так как условия определения гибридной матрицы , близки к физическим работам транзистора

Гибридная матрица применяется при смешанном соединении четырехполюсников – по входу последовательно и параллельно по выходу. H =  Σ (|H_i|)

Таблица соединений четырехполюсников:                                                             

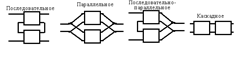Матрица волновой теории четырехполюсников.