А М – эмпирические коэффициенты для каждого из слоев измерены и находятся в справочнике.Т – абсолютная температура.Un – напряжение на переходе.Если модель дискретная, то в ней учитываются индуктивности выводов и емкости контактов. 2.Ск – емкость контактов.Сн – емкость корпуса.L1, L2 – индукт выводов.Если диод интегральный, то его представляют как полную структуру биполярного транзистора, включенного в диодном исполнении.
Метод переменных состояния.
.Если
в схеме встречаются нелинейные элементы, то этот метод не подходит, а
используется метод переменных состояния. Он позволяет описать схему с помощью
системы в виде двух матричных уравнений:![]()
![]() V –
вектор фазовых переменных называется переменным состояния. Q –
векто, характеризует входное воздействиеF – вектор,
характеризует выходные параметры. L и М – постоянные действительные
матрицы, размер которых описывается размером схемы.
V –
вектор фазовых переменных называется переменным состояния. Q –
векто, характеризует входное воздействиеF – вектор,
характеризует выходные параметры. L и М – постоянные действительные
матрицы, размер которых описывается размером схемы.
Данная система диф. Уравнений первого порядка наз. Системой для переменных состояния в нормальной форме.
Алгоритмическую реализацию данного метода во многом определяет выбор вектора V.
![]() (Ф)
(Ф)![]()
IR-Id=0
Ik=UR/R Id=Io*(exp(α*U)-1) U=E-Uk. Выразим
U из вышеприведенных уравнений -.(Ф) .![]()
Условие,
по которому выбирают одно из уравнений написанных выше. Данное описание НУ
используется тогда, когда решение не лежит на оси абсцисс.Все данные НУ
решаются численными методами с какой-то заданной точностью. Если схема
описывается уравнением (1), то используются следующие численные методы :
метод хорд, половинного деления, метод Ньютона. Самый простой – метод половинного
деления. Самый быстродействующий –метод Ньютона.Недостатки: необходимо взять
первую производную, нужно выбрать точку в окрестности решения. Используется ,
если легко выполнимы эти условия.. Метод Хорд. 1. Выбираем интервал (U1, U2) f(U1)*f(u2)<0
(*) Данное условие проверяет , что точка находится в данном интервале.2.
Записываем уравнение прямой, соединяющей эти две точки: ![]() . |f(u)|<=ε –
Если это условие не выполняется, то U1=U и т. д. Из
уравнения прямой находим значения:
. |f(u)|<=ε –
Если это условие не выполняется, то U1=U и т. д. Из
уравнения прямой находим значения:![]()
1) ![]() 2)
2) ![]() 3)
3) ![]()
Метод половинного деления. 1) U=(U2+U1)/2 |F(U)|< ε Если f(U1)*f(u)>0 , то U1=U, если условие не выполняется, то U2=U. Метод Ньютона. 2) df/dU<1 Условие, если не выполняется, то U=U-ΔU f(U)<ε. Метод итераций.3) Позволяет найти решение не лежащее на оси абсцисс. В методе итераций задается точка в окрестности решения. Далее находится функция (U) проверяется условие : |U- φ(U)|<ε , если выполняется , то это решение, иначе продолжаем итерации.
Математические модели радиоэлектронных систем.
Фазовые переменные , которые полностью характеризуют модель, являются функцией комплексной частоты. При моделировании РЭС в частотной области используется метод комплексных амплитуд, который заключается в следующем: при синусоидальном воздействии на схему любой сложности в установившемся режиме, токи и напряжения данной схемы могут быть представлены в виде сумм синусоидальных составляющих основной частоты w , 2w, 3w. Такой подход называется спектральным анализом. В качестве фазовых переменных принимаются напряжения и токи не только на отдельных компонентах , но и на входах и выходах четырех или многополюсников. К входным параметрам РЭС в частотной области относятся различные функции цепей. Связи между выходными параметрами РЭС.
K(jw) – комплексный коэффициент передачи, то частотная и импульсная характеристика g(t) связаны между собой преобразованием Фурье.
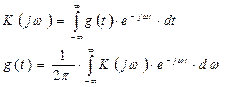 K(jω) = |
K(jω) = |
K(jω)|*exp(jφ)
![]()
![]() Для аналоговых сигналов
соотношение коэффициента передачи непрерывна, а для импульсных сигналов
применяются специально разработанные алгоритмы дискретного преобразования
Фурье , в этом случае импульсная и переходная характеристика связаны между
собой
Для аналоговых сигналов
соотношение коэффициента передачи непрерывна, а для импульсных сигналов
применяются специально разработанные алгоритмы дискретного преобразования
Фурье , в этом случае импульсная и переходная характеристика связаны между
собой
Если на устройство происходит подача сигнал, то выходной сигнал можно получить с помощью использования интеграла Дюамеля или интеграла свертки:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.