Задача №1
Динамическое вписывание машины в кривую
Цель расчета: проверить возможность пропуска машины по участку пути с заданной скоростью (по нагрузке на головку рельса).
Исходные данные: масса машины m = 110 т; скорость движения машины u = 100 км/ч; расчетный радиус кривой R = 1000 м; расстояние до центра масс l = 7 м, h = 2 м.
Условия расчета: машина проходит кривую расчетного радиуса с заданной скоростью, проверены нагрузки от колеса на головку рельса.
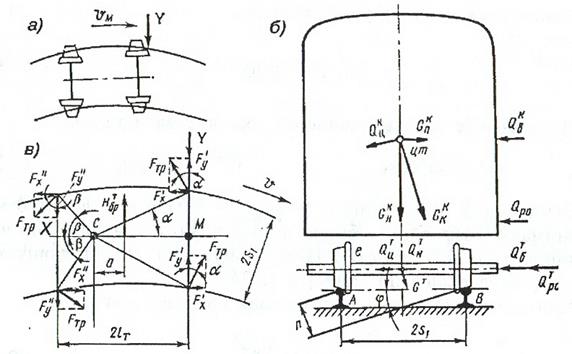
а – положение тележки в кривой; б – приложенные силы; в – действие сил трения
Рисунок 1 – Схема динамического вписывания
На расчетной схеме рассмотрен случай равномерного нагружения ходовых тележек в горизонтальной и вертикальной плоскостях.
Для определения направляющей реакции у составлены два уравнения:
Sу = 0: ![]() (1)
(1)
SМк =
0: ![]() (2)
(2)
Суммарная поперечная сила, приходящаяся на одну тележку, при условии, что силы действуют в одной плоскости:
![]() (3)
(3)
где Qцк , Qцт – центробежная сила, действующая на кузов и тележку; G’к , G’т – составляющие сил тяжести кузова и тележки; Wв– ветровая нагрузка; nт– число колес.
В общем случае центробежная сила:
Q = m×υ2/R, (4)
Составляющие сил тяжести:
G’ = G × sin φ = G × h /2s1 , (5)
где h– возвышение наружного рельса; 2s1–расстояние между кругами катания колёсной пары, 2s1 = 1600 мм.
h = 1,25 ×υ2/R. (6)
h = 1,25 × 100 2/1000 = 12,5 мм
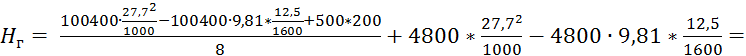 = 88 кН.
= 88 кН.
Центробежная сила, действующая на тележку:
![]() (7)
(7)
![]()
![]() .
.
Сила трения скольжения между каждым колесом и рельсом в момент его поворота относительно мгновенного центра вращения:
![]() (8)
(8)
где fст– коэффициент трения скольжения, fст = 0,25.
![]() 73,3 × 0,25 = 18,3
кН.
73,3 × 0,25 = 18,3
кН.
Неизвестные Y и а найдены с использованием графиков, изображенных на рисунке 2.
Для нахождения Yотношение НГ к Fтр :
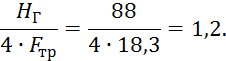
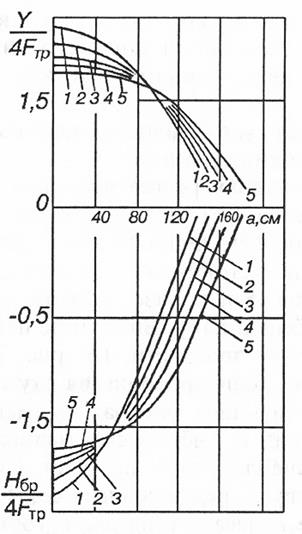
Рисунок 2 – Графики для определения силы у при длине тележки:
1 – 180 см; 2 – 210 см; 3 – 240 см; 4 – 270 см; 5 – 300 см.
По нижнему графику найдена а = 65 см, при длине тележки 180 см. Зная а, по верхнему графику найдено Y/ 4Fтр = 2,2. Поскольку 4Fтр известно, то Y = 2,2 × 4Fтр = 2,2 × 4 × 18,3 = 161 кН.
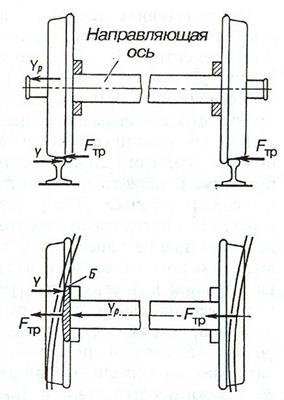
Рисунок 3 – Силы, действующие на колесную пару
Следовательно, на направляющую колесную пару в кривой действуют силы, приложенные (см. рис. 3): Y–к гребню колеса, Y– 161 кН; Fтр– в месте контакта колеса с каждым рельсом, Fтр = 18,3 кН; Yр– рамная, направленная по оси колесной пары Yр = Y - 2Fтр = 1041 - 2 × 18,3 = 124 кН.
Допустимые значения Y:
![]() (9)
(9)
где Fк– допустимая нагрузка на колесную пару, Fк = 230 кН; e–постоянная, e = 10 кН.
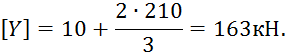
![]()
Пропуск машины с заданными параметрами по кривой радиуса 1000 м со скоростью 100 км/ч возможен.
Задача №2
Проверка машины на опрокидывание
Цель расчета: проверить устойчивость машины против опрокидывания.
Исходные данные: масса машины m = 110 т; скорость движения машины u = 100 км/ч; расчетный радиус кривой R = 1000 м; расстояние до центра масс l = 7 м, h = 2 м.
Условия расчета: машина движется по кривой расчетного радиуса с заданной скоростью.
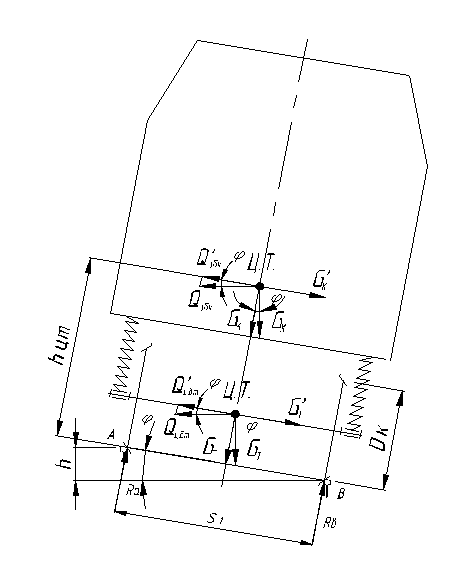
Рисунок 4– Расчетная схема для определения устойчивости машины
Коэффициент устойчивости n:
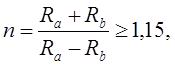 (10)
(10)
где RA , RB– реакции, определяемые из условия равновесия.
Суммы моментов всех сил относительно точек А и В:
![]()
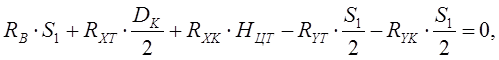 (11)
(11)
![]()
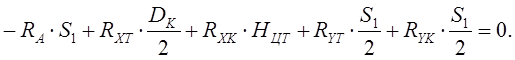 (12)
(12)
где S1 – расстояние между кругами катания
колес,S1 = 1600
мм; Dk– диаметр колеса,Dk = 1050 мм; HЦТ– высота до центра тяж ести,HЦТ = 2 м; ![]() – сумма проекций сил, действующие на
кузов и тележку ,в горизонтальной и вертикальных плоскостях.
– сумма проекций сил, действующие на
кузов и тележку ,в горизонтальной и вертикальных плоскостях.
![]() ; (13)
; (13)
![]() ; (14)
; (14)
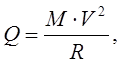 (15)
(15)
где М – масса, МТ = 4800 кг – масса тележки, МК = 100400 кг – масса кузова;V– скорость движения машины, V = 100 км/ч = 27,7 м/с;R– радиус кривой, R = 1000 м.
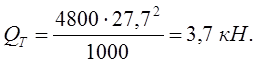
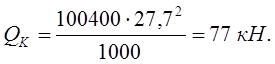
![]()
![]()
![]() (16)
(16)
![]() (17)
(17)
![]()
![]()
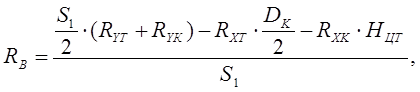 (18)
(18)
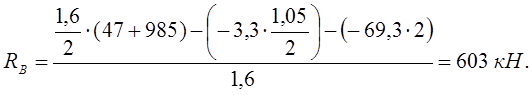
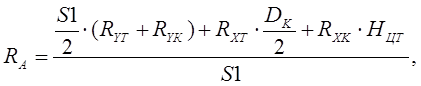 (19)
(19)
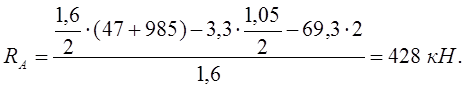
Коэффициент устойчивости n:
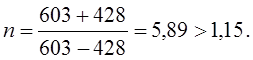
Вывод: устойчивость достаточна для движения заданной машины по кривой, радиусом 1000 м и скоростью 100 км/ч.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.