где a— коэффициент, учитывающий соответствие циклов касательного (от крутящего момента Т) и нормального (от изгибающего момента М) напряжений; при реверсивной работе привода a = 1, для нереверсивного привода в предположении частого включения и выключения электродвигателя a = 0,7.
Е. Определение диаметра вала в опасном сечении.
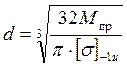 , (191)
, (191)
где ![]() — допускаемое нормальное
напряжение, для наиболее распространенных марок сталей
— допускаемое нормальное
напряжение, для наиболее распространенных марок сталей ![]() =
50...60 МПа; верхнее значение принимают для вала-шестерни из высокопрочного
материала.
=
50...60 МПа; верхнее значение принимают для вала-шестерни из высокопрочного
материала.
Ж. Конструирование вала с окончательным назначением диаметров во всех характерных сечениях вала.
Результаты, полученные из формул (176) и (190), могут оказаться различными. Предпочтение следует отдавать приближенной методике расчёта как более точной. Вероятно превалирование соображений конструктивного плана.
Пример 17. Выполнить приближённый расчёт промежуточного вала двухступенчатого коническо-цилиндрического редуктора (рис. 37) по исходным данным примеров 1, 5, 9 и 16. Крутящий момент TII = 84 Н·м. Материал вала сталь 40Х, термообработка – улучшение. Расстояния между линиями действия сил (из эскизной компоновки): l1 = 70 мм, l2 = 60 мм, l3 = 50 мм. Работа нереверсивная. Параметры передач приведены в табл. 27.
Таблица 27
Параметры передач (выборка из табл. 12 и 17).
|
Параметры |
Величины |
|
|
Коническое колесо |
Цилиндрическая шестерня |
|
|
Делительный диаметр d, мм |
dm2 =171,77 |
d1 = 65,57 |
|
Окружное усилие в зацеплении Ft, H |
Ft1 =1032 |
Ft2 = 2562 |
|
Радиальное усилие в зацеплении Fr, H |
Fr1 = 102 |
Fr2 = 956 |
|
Осевое усилие в зацеплении Fa, H |
Fa1 = 362 |
Fa2 = 572 |
Решение.
1) Составляем расчётную схему вала (рис. 37). На схеме нагружения валов (рис. 37, а) действующие силы приложены в соответствии с кинематической схемой на рис. 3 (после поворота на 90º): силы на коническом колесе приложены в верхней точке, а на цилиндрической шестерне – в нижней точке зацепления. Окружные силы Ft показаны действующими в одном направлении, но создают они крутящие моменты противоположного направления. Направление Ft1 определяет направление вращения вала. Сила Ft2 на шестерне создаёт момент против направления вращения. Осевая сила Fa1 направлена с сторону основания конуса, а сила Fa2 – ей противоположно для уменьшения нагрузки на подшипник. Схема нагружения преобразована после приведения действующих сил к оси вала на две расчётные схемы сил, действующих в двух плоскостях. Приведение сил выполнено по следующим правилам:
а) радиальные силы Fr проходят через ось вала, к которой они и приложены без добавления моментов;
б) осевые силы приведены к оси с добавлением сосредоточенных моментов т = Fa·d/2; в) окружные силы приведены к оси с добавлением крутящих моментов TII;
г) схемы и эпюры выполнены на отдельном листе.
2) Определяем реакции и моменты в плоскости ZOY. Силы, действующие в направлении Z, показаны на рис. 37, б. Реакции опор R1zи R2z определены из двух уравнений равновесия. Третье уравнение использовано для проверки. Сосредоточенные моменты:
m1= Fa1·dm2/2 = 362·171,77/2 = 31090 Н·мм = 31,1 Н·м;
т2= Fa2·d1/2 = 572·65,57/2 = 18753 Н·мм = 18,8 Н·м.
Уравнение моментов сил относительно опоры 1:
![]() , откуда
, откуда
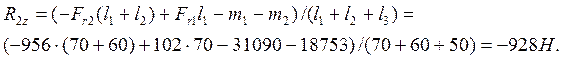
Направление реакции R2z противоположно изображённому на рис. 37, б. Уравнение проекций:
![]() откуда
откуда
![]()
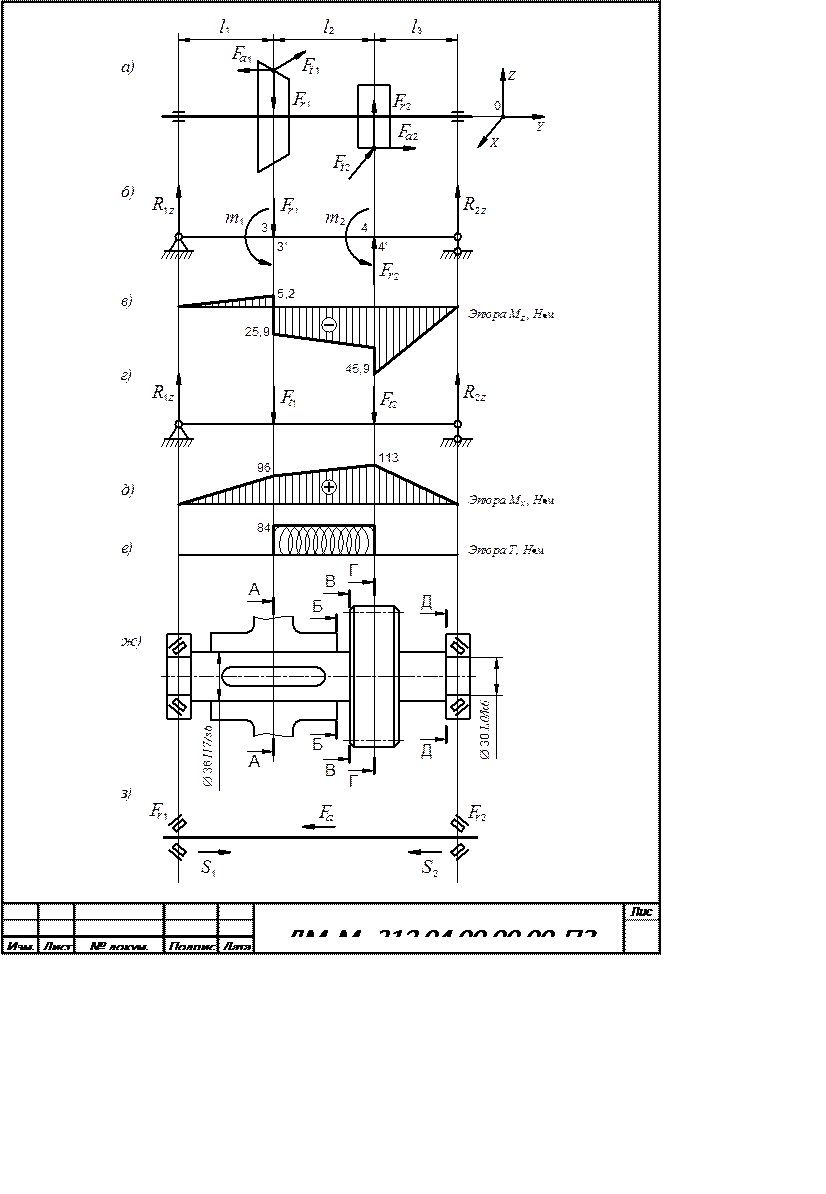
Рис. 37. Расчётные схемы вала II
Проверочный расчёт выполнен по уравнению моментов сил относительно опоры 2:
![]()
![]()
![]()
Полученное значение близко к нулевому. Эпюры изгибающих моментов (рис. 37, в) построены на сжатом волокне. Значения моментов Mz:
М1z = 0; ![]()
![]()
![]()
![]()
![]()
На эпюре Мzпод сосредоточенными моментами будут скачки, равные модулям моментов т1 и т2.
В направлении XOY действуют силы Ft1 и Ft2 (рис. 37, г), которые для удобства расчётов совмещены с вертикальной плоскостью. Искомые реакции опор определены аналогично плоскости ZOY из двух уравнений равновесия:
![]() откуда
откуда
![]()
![]() откуда
откуда
![]()
3)Изгибающие моменты в направлении X:
М1x = 0; ![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.