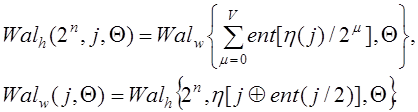 (1.2.28) и (1.2.29)
(1.2.28) и (1.2.29)
Здесь ![]() , а суммирование выполняется по модулю 2.
На рис 1.2.3 изображены первые шестнадцать функций Уолша.
, а суммирование выполняется по модулю 2.
На рис 1.2.3 изображены первые шестнадцать функций Уолша.
Рассмотрим
полную ортогональную, ортонормированную на отрезке [0,1] систему функций Хаара,
определяемую [16] следующим образом: ![]() и, если
и, если ![]() то
то
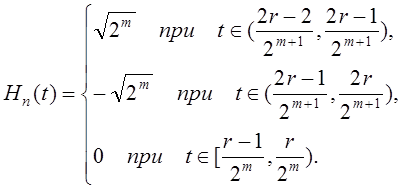 (1.2.30)
(1.2.30)
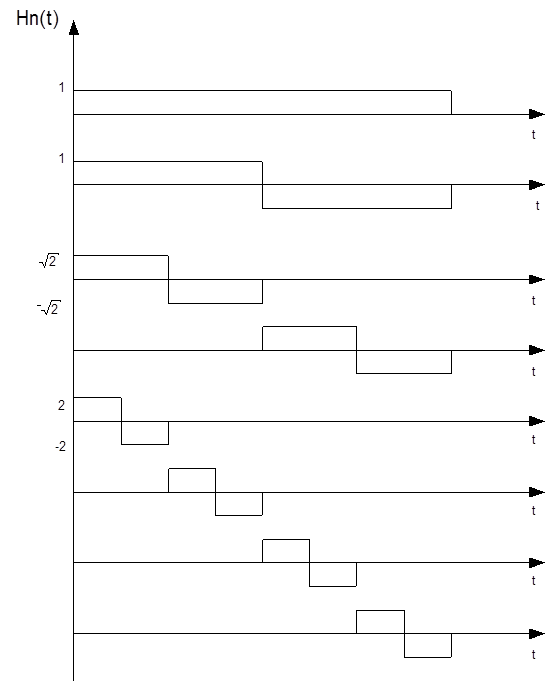 |
Отметим, что в точках разрыв функции Харра (рис. 1.2.4) равны полусумме пределов справа и слева, а на концах отрезка [0,1] – своим предельным значениям изунутри отрезка.
1. ОПИСАНИЕ ДВУХМЕРНОЙ СИСТЕМЫ ФУНКЦИЙ Ваh.
Позвольте нам обобщить вышеупомянутое описание в двумерной системе функций. Рассмотреть следующую систему сложных функций
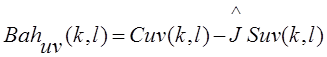 (11)
(11)
Которые определены на дискретном множестве
M={(k ,l): k=0,1,2,…,![]() ,
l=0,1,2,…,
,
l=0,1,2,…, ![]() }
}
Где u = 0,1,2,3,…,n-1,
v = 0,1,2,3,…,n-1,
![]() - номер вертикальных и горизонтальных
подинтервалов, состоящих из точка приблизительно двумерный дискретный сигнал f(k,l), который
должен быть проанализирован. Другими словами,
- номер вертикальных и горизонтальных
подинтервалов, состоящих из точка приблизительно двумерный дискретный сигнал f(k,l), который
должен быть проанализирован. Другими словами, ![]() - минимум целочисленное положительное номер, для которого
выражения следования являются правильными:
- минимум целочисленное положительное номер, для которого
выражения следования являются правильными:
![]()
Так что период двумерного сигнала f(k,l) - квадрат:
{(k,l): 0![]() k
k![]()
![]() , 0
, 0![]() l
l![]()
![]() }
}
Функции Cuv(k,l) и Suv(k, l) определены следующим способом:
![]()
![]() , когда
, когда ![]()
Когда ![]() и
и ![]() , который является
, который является ![]() ,
мы имеем:
,
мы имеем:
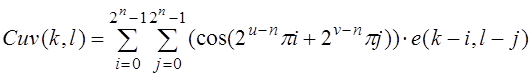
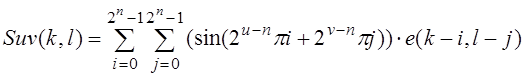
Где ![]() является
импульсом модуля, задержанным мной и сменами i и j:
является
импульсом модуля, задержанным мной и сменами i и j:
![]()
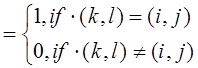
Как в одномерном случае система сложных функций (11) согласно формуле Аулера может теперь быть легко выражена через показательные функции:
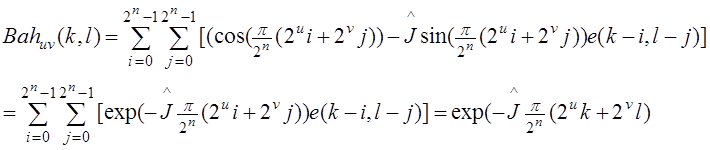 (12)
(12)
Где k изменяется от 0 до ![]() с
шагом, равным
с
шагом, равным ![]() , L изменяется от 0 до
, L изменяется от 0 до ![]() с
шагом, равным
с
шагом, равным ![]() . Обратите внимание, что необходимо сделать
циклические сдвиги некоторыми из функций (12), относительно проанализированному
сигналу системы сложных функций (11)
может перезаписаный следующим способом:
. Обратите внимание, что необходимо сделать
циклические сдвиги некоторыми из функций (12), относительно проанализированному
сигналу системы сложных функций (11)
может перезаписаный следующим способом:
![]() ,
,
u=0,1,2,…,n-1, v=0,1,2,…,n-1.
Где ![]() и
и ![]() -
функции Cuv(k,l)
и Suv(k,l), перемещенный
-
функции Cuv(k,l)
и Suv(k,l), перемещенный
Su и Sv делят на интервалы в горизонтальном и вертикальном направлениях соответственно.
Примечание, что:
Если u = v = 0 , то Su = Sv = 0;
Если u=0 и v![]() 0 , то Su=0 и Sv
изменяется от 0 до
0 , то Su=0 и Sv
изменяется от 0 до ![]() с шагом равный 1;
с шагом равный 1;
Если ![]() и v =
0 , то Sv=0 и Su изменяется от 0 до
и v =
0 , то Sv=0 и Su изменяется от 0 до ![]() с шагом равный 1;
с шагом равный 1;
Если ![]() и
и ![]() то Su изменяется от 0 до
то Su изменяется от 0 до ![]() с шагом, равным 1 и Sv изменяется от 0 до
с шагом, равным 1 и Sv изменяется от 0 до ![]() с шагом, равным
1.
с шагом, равным
1.
В этом случае двумерный спектр с амплитудной частотой проанализированного сигнала может быть вычислен согласно выражению следования:
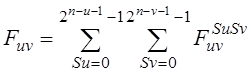 (13)
(13)
Где
![]()
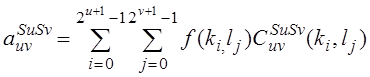
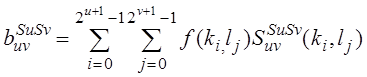
u = 0,1,2,3,…,n-1, v = 0,1,2,3,…,n-1.
![]() - значение проанализированного сигнала в точке,
- значение проанализированного сигнала в точке, ![]() .
.
Чтобы испытать предложенный подход к формированию спектра с амплитудной частотой, проводились несколько экспериментов с помощью письменных программ. Основная цель – эксперимент должен подтвердить, что теоретические результаты соответствуют действительности. В результате проведенных экспериментальных исследований было установлено, что амплитудно – частотный спектр, полученный с помощью предложенной системы сложных функций действительно не зависит от смен сигнала.
В современных условиях развития вычислительной техники и всеобщей компьютеризации становиться наиболее актуальной проблема быстрого ввода информацией. Особенно если речь идет о ввода различных иероглифов через клавиатуры. Поэтом необходимо разработать методы быстрого ввода иероглифов. Один из методов быстрого ввода иероглифов это с помощью сканера сканирует тексты и после чего обрабатывает специальный программ. Т.е распознавание тексты в виде изображения. Поскольку большеннстве таких программы базируется на алгоритмы наложения изображения и затем вычисляется корреляции по модуль. Однако этот метод не подходит в случае иероглиф, поскольку во первых иероглиф состоит из десятки тысяча элементов, во вторых у иероглифы имеет специфические структуры. Что не дает быстрого распознавание изображения (поскольку нужен создавать элементный баз, а они состоит из десятков тысяча), и точности (поскольку есть такие иероглифы который друг другу очень похоже). Один из наиболее перспективный метод это с помощью спектрального анализа распознавать иероглифы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.