Формирование инвариантных признаков для распознавания иероглифов на основе спектральных методов, страница 4

Среди различных аспектов обобщенной спектральной теории, оказывающих непосредственное влияние на методы синтеза алгоритмических и аппаратных средств особое место занимают вопросы конструктивного формирования систем базисных функций. Представления о генерировании последних претерпели существенные изменения в результате исследования вопросов синтеза ортогональных базисов на основе обобщенного спектрального ядра [21]. Варьируя параметры спектрального оператора, можно плавно переходить от одного базиса к другому, что позволит на практике при обработке сигналов вплотную подойти к решению задачи оптимального выбора базисной системы функций и рассмотреть с единых позиций вопросы синтеза средств генерации. Отметим, что функции Виленкина – Крестенсона (ВКФ), являющиеся обобщением ДЭФ и кусочно-постоянных функций Уолша, как правило, используются в задачах анализа и синтеза систем р - значной логики [32] и практически не применяются при обработке сигналов. Одна из основных причин заключается в сложности их формирования и отсутствии методик синтеза соответствующих аппаратных средств.

1.Литературный обзор.     

1.1 формирование функций Виленкина – крестенсона и обобщенных функций Хаара.

Система ВКФ  , определяемая обычно на конечном интервале , при  включает функции Уолша , при  ДЭФ. Аналистически ВКФ могут быть получены с помощью обобщенных функций Радемахера

,                                                  (1.1.1)

где -простое число; -мнимая единица; ;     -целая часть.

Базисная система ВКФ на интервале  определяется как произведение соответствующих обобщенных функций Радемахера, т.е.

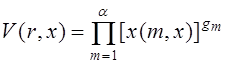.                                                         (1.1.2)

Здесь -номер ВКФ; -разрядные коэффициенты в -ичном представлении числа

Приведем без доказательств основные свойства системы ВКФ ( доказательства содержатся в работах [32,21]) : 1) действительная и мнимая ее части имеют  уровней квантования (по величине) ; 2) матрица преобразования Виленкина-Крестенсона является симметрической, т.е. для ее строк и столбцов справедливо соотношение  3) ВКФ-система периодическая с периодом  4) она является полной и ортогональной на интервале определения :

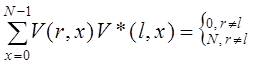
(* означает комплексное сопряжение); 5) ее модуль |и среднее значение при 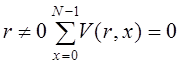; 6) система является мультипликативной, т.е. образует абелеву группу относительно операции умножения: 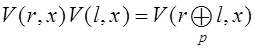; 7) матрица преобразования Виленкина-Крестенсона унитарна.

Для и матрицы ВКФ в различных системах упорядочения (Пэли, Качмажа, Адамара) имеют следующий вид: а) система ВКФ-Пэли (рис. 1.1.1)

1.2. Системы ортогональных функций фурье, уолша, хаара.

Значительная часть задач цифровой обработки временных последовательно- стей связана с применением преобразования Фурье с тригонометрической системой базисных функций, являющихся частным случаем ВКФ. В этих задачах Фурье-преобразование играет важную роль как необходимый инструмент к определению собственных и взаимных спектральных и временных характеристик процессов, сверток и передаточных функций динамических обьектов.

Аналогом  комплексных экспоненциальных функций в дискретном случае являются дискретные экспоненциальные функции(ДЭФ)

        (1.2.1)

Основные свойства ДЭФ приведены в работах . В последние годы в связи с интенсивным развитием цифровой вычислительной техники внимание исследователей стала привлекать полная ортогональная система прямоугольных функций Уолша, принимающая два значения: +1и –1. Для базиса Уолша существуют ускоренные процедуры, что делает его конкурентоспособным по отношению к традиционно используемому быстрому Фурье-преобразованию.

Функции Уолша  образуют счетное множество ортогональных периодических прямоугольных функций, где -аргумент, нормированный к периоду -частота следования. Различают три системы упорядочения функций Уолша: двоично-упорядоченные, или функции Уолша-Пэли  частотно-упорядоченные, или функции Уолша-Качмажа  Кронекер-упорядочнные, или функции Уолша-Адамара . Основные свойства системы Уолша приведены в работах .