Двойчно –
упорядоченные, или функции Уолша-Пэли,
могут быть получены из функций Радемахера ![]() , которые,
являясь подмножеством системы Уолша, образуют неполное
множество периодических ортогональных функций и определяются как
, которые,
являясь подмножеством системы Уолша, образуют неполное
множество периодических ортогональных функций и определяются как
![]() (1.2.2)
(1.2.2)
или
![]()
где ![]() означает целую часть от
означает целую часть от ![]()
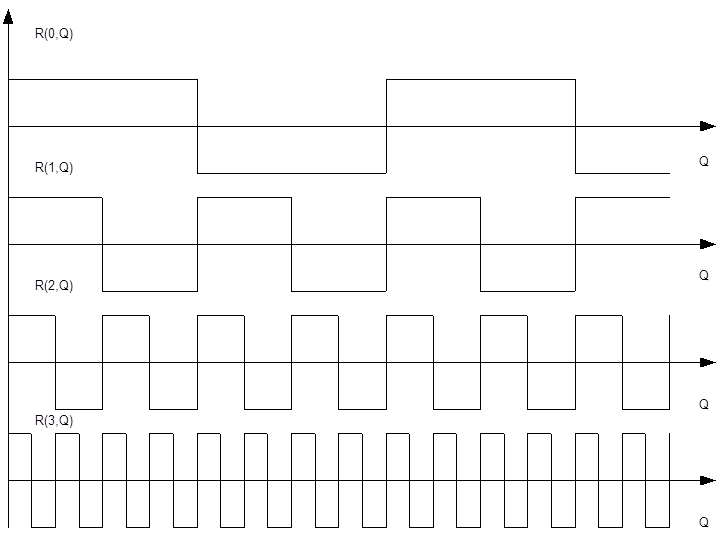 |
Рис. 1.2.1.
Функции Радемахера ![]() .
.
На рис. 1.2.1 показаны первые четыре функции Радемахера, которые, являясь нечетными, аналогично функциями Уолша принимают два значения +1 и –1.
Запишем выражение для функций Уолша-Пэли в виде произведения функций Радемахера
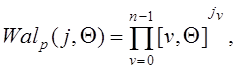 (1.2.3)
(1.2.3)
где
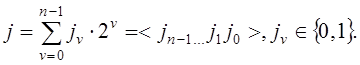
Например, если ![]() то
то ![]() Для произведения двух соответствующих
функций Уолша-Пэли будем иметь
Для произведения двух соответствующих
функций Уолша-Пэли будем иметь
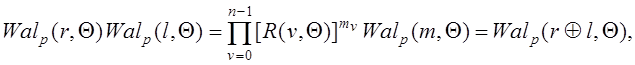 (1.2.4)
(1.2.4)
где ![]() -операция сложения по модулю два;
-операция сложения по модулю два; ![]() Из формулы
(1.2.3) и определения функций Радемахера следует
Из формулы
(1.2.3) и определения функций Радемахера следует
![]() (1.2.5)
(1.2.5)
Тогда получим следующее рекуррентное соотношение для системы Уолша – Пэли:
![]()
или
![]() (1.2.6)
(1.2.6)
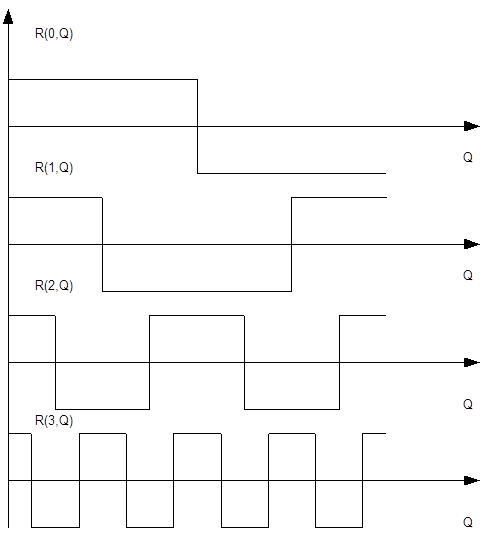 |
Рис.
1.2.2. Четные функции Радемахера ![]() .
.
![]()
![]() (1.2.7)
(1.2.7)
В
свою очередь для функций Радемахера ![]() справедливо
соотношение
справедливо
соотношение
![]() (1.2.8)
(1.2.8)
Функции
Уолша - Качмажа определим в виде произведения соответствую- щих функций ![]()
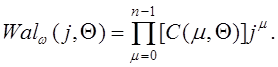 (1.2.9)
(1.2.9)
Из (1.2.9) для ![]() будем иметь
будем иметь
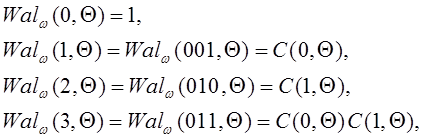 (1.2.10)
(1.2.10)
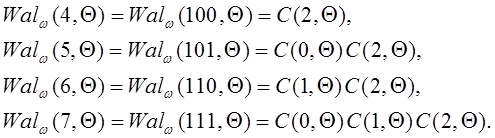
Для функций Уолша- Качмажа справедливы следующие выражения:
![]() (1.2.11)
(1.2.11)
![]() (1.2.12)
(1.2.12)
Рекуррентное соотношение для системы Уолша – Качмажа будет иметь вид
![]() (1.2.13)
(1.2.13)
где ![]() По аналогии с тригонометрическими функциями
По аналогии с тригонометрическими функциями
![]() функции Уолша – Качмажа
подразделяются
функции Уолша – Качмажа
подразделяются ![]() на четные
на четные ![]() и нечетные
и нечетные ![]()
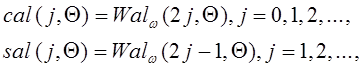 (1.2.14)
(1.2.14)
(1.2.15) или
![]() (1.2.16)
(1.2.16)
Теорему умножения для (1.2.14) и (1.2.15) можно записать следующим образом:
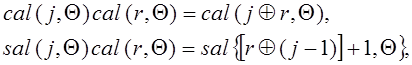
(1.2.17)
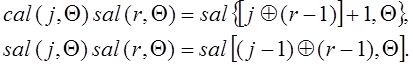
Третья
система- функции Уолша- Адамара. Они могут быть
получены из квадратных ортогональных матриц размерностью ![]() с элементами +1 и –1,
определяемых рекуррентно в виде
с элементами +1 и –1,
определяемых рекуррентно в виде
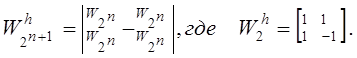
Для ![]()
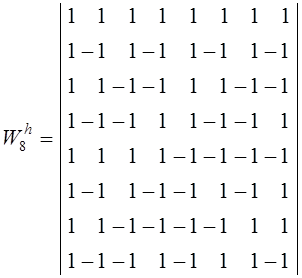
Элементы ![]() матрицы
матрицы ![]() вычисляются
по формуле
вычисляются
по формуле
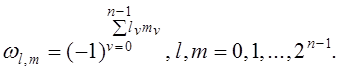
Функции Уолша –
Адамара могут быть также определены [![]() ] как
] как
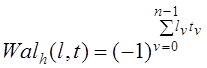 (1.2.18)
(1.2.18)
или в виде произведения соответствующих функций Радемахера
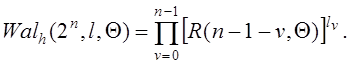 (1.2.19)
(1.2.19)
Из (1.2.19) для ![]() имеем
имеем
![]() (1.2.20)
(1.2.20)
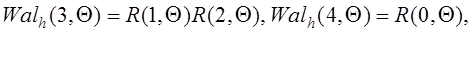
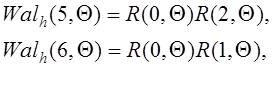
![]()
Элементы матрицы
Адамара размерностью ![]() можно найти из элементов этой
матрицы меньшей размерности с помощью соотношения
можно найти из элементов этой
матрицы меньшей размерности с помощью соотношения
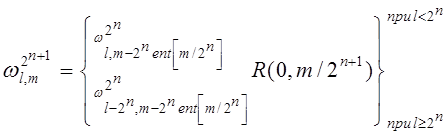
Тогда можно определить рекуррентное соотношение, справедливое для системы Уолша – Адамара:
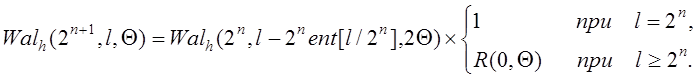 (1.2.21)
(1.2.21)
Для функций Уолша одной группы справедлива следующая теорема умножения:
![]() (1.2.22)
(1.2.22)
Рассмотрим теперь вопрос отображения различных систем функций Уолша. Подставляя (1.2.8) в (1.2.9), получаем отображение системы Уолша – Пэли на систему Уолша – Качмажа:
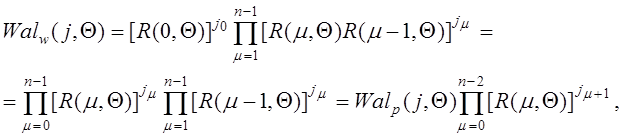 (1.2.23) т.е.
(1.2.23) т.е.
![]() (1.2.24)
(1.2.24)
Обратное отображение задается соотношением
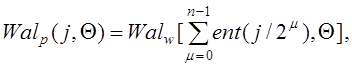 (1.2.25)
(1.2.25)
где суммирование выполняется по модулю 2.
Для систем Уолша – Пэли и Уолша – Адамара существуют взаимнооднозначные отображения
![]() (1.2.26)
(1.2.26)
![]()
![]()
![]()
![]()
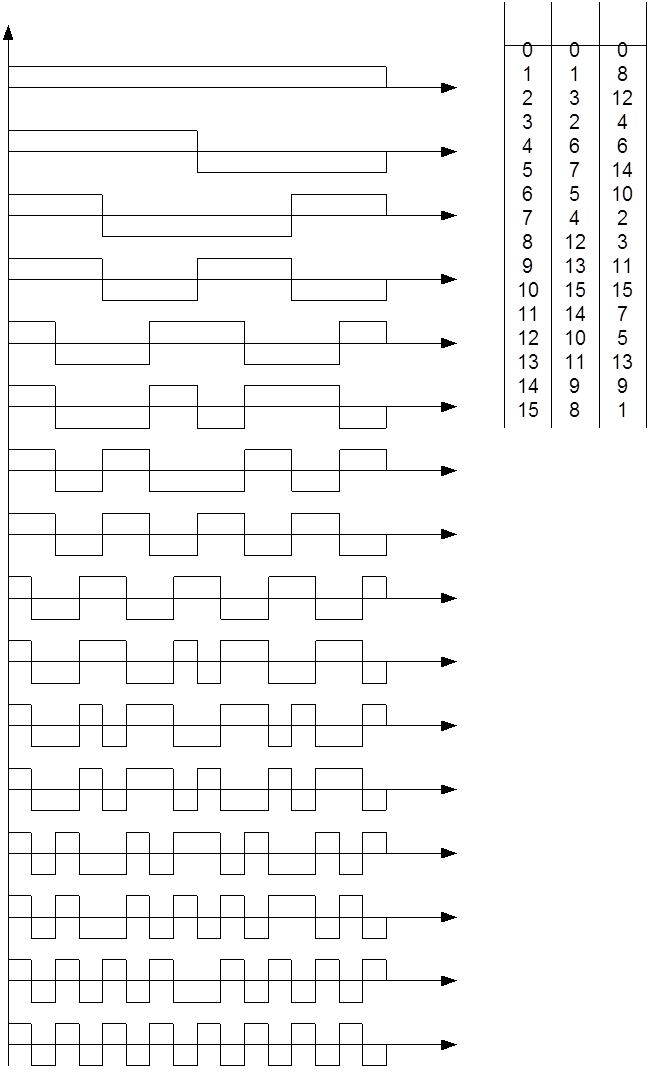 |
![]() (1.2.27)
(1.2.27)
где ![]() разрядное представление j
с обратным двоичным порядком. Аналогично, используя формулы (1.2.24)-(1.2.27),
получаем следующие соотношения:
разрядное представление j
с обратным двоичным порядком. Аналогично, используя формулы (1.2.24)-(1.2.27),
получаем следующие соотношения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.