

Цель работы: исследование устойчивости системы по критерию Найквиста.
Структурная схема:
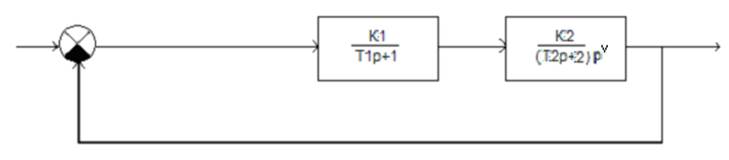
1) V = 0; T1 = 0.05; T2 = 0.01
Передаточная функция этой
системы равна 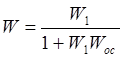 (1)
(1)
Где ![]() ,
а
,
а 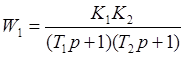
Подставляя эти выражения в (1) и выражая знаменатель в виде полинома, получим характеристическое уравнение:
![]() (2)
(2)
1. K1 = 1.2; K2 = 1.2 2. K1 = 2; K2 = 3
Подставляя в
характеристическое уравнение разомкнутой системы вместо ![]()
![]() получим выражение вида
получим выражение вида ![]() .
Изобразим его на комплексной плоскости.
.
Изобразим его на комплексной плоскости.
Графики переходных процессов
при этих коэффициентах могут быть получены путем применения обратного преобразования
Лапласа над передаточной функцией ![]() .
.
Проверим систему на устойчивость с помощью критерия Гурвица. Матрица коэффициентов характеристического уравнения системы имеет вид:
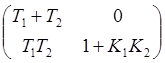 ,
соответственно первый и второй определители Гурвица равны:
,
соответственно первый и второй определители Гурвица равны: 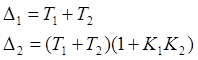
случай 1. случай 2.
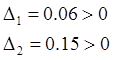
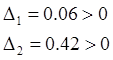
2) V = 1; T1 = 0.05; T2 = 0.01
Передаточная функция этой
системы равна 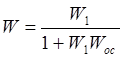 (1)
(1)
Где ![]() ,
а
,
а 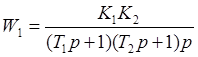
Подставляя эти выражения в (1) и выражая знаменатель в виде полинома, получим характеристическое уравнение:
![]() (2)
(2)
1. K1 = 4; K2 = 5 2. K1 = 5; K2 = 24 3. K1 = 10; K2 = 18
Подставляя в
характеристическое уравнение разомкнутой системы вместо ![]()
![]() получим выражение вида
получим выражение вида ![]() .
Изобразим его на комплексной плоскости.
.
Изобразим его на комплексной плоскости.
Графики переходных процессов
при этих коэффициентах могут быть получены путем применения обратного
преобразования Лапласа над передаточной функцией ![]() .
.
Проверим систему на устойчивость с помощью критерия Гурвица. Матрица коэффициентов характеристического уравнения системы имеет вид:
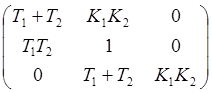 ,
соответственно первый, второй и третий определители Гурвица равны:
,
соответственно первый, второй и третий определители Гурвица равны: 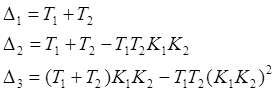
случай 1. случай 2. случай 3.
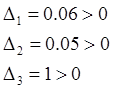
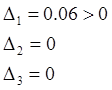
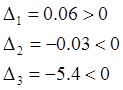
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.