Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 3, страница 3

  

Момент сопротивления для круглого сечения

Из условия прочности:=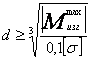

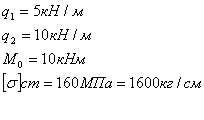
Задача №2

Дано

Определяем неизвестные реакции опор составляя уравнение статики:

Проверка

                              5,25-25+50-30,25=0

Эпюра Q(x)

Участок №1                

    (слева)                    Уравнение для Q(x)

Q(x -  уравнение наклонной прямой

 X

Эпюра  пересекает ось X, меняя знак с плюса на минус.

Найдем координату X,  при которой  Q

Участок №2             

   (справа)                  Уравнение для Q(x)

Q(x -  уравнение наклонной прямой

X

Эпюра  пересекает ось X, меняя знак с плюса на минус.

Найдем координату X,  при которой  Q

Эпюра М(х)

Участок №1                

    (слева)                    Уравнение для М(x)М(x -  уравнение параболы

 X

Для нахождения третьей точки параболы, воспользуемся дифференциальной зависимостью:

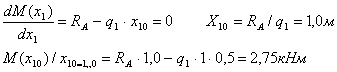
Участок №2             

   (справа)                  Уравнение для M(x)

M(x -  уравнение параболы

X

Для нахождения третьей точки параболы, воспользуемся дифференциальной зависимостью:

М(x/

     В точке приложения сосредоточенного момента МкНм на эпюре М(х) будет наблюдаться скачок, равный величине этого момента.

Условие прочности