Построение эпюр для балки по заданным параметрам, страница 5

В точке приложения сосредоточенной силы Р=20kH, на эпюре Q(x) будет наблюдаться скачок, равный величине этой силы.

Участок №4

(справа)

Уравнение для :

 - - не зависит от  прямая, паралледьная оси Х.

В точке приложения реакции опоры =5kH,на эпюре Q(x) будет наблюдаться скачок, равный велечине этой реакции.

Эпюра М(х):

Участок №1

(слева)

Уравнение для :

 - уравнение параблы

Для построения этой параболы найдем три ее точки

 - (шарнир”B” – слева)

Для нахождения третьей точки параболы воспользуемся дифференциальной зависимостью:

Вычислим производную от , приравняем ее к нулю и найдем значение координаты ,при котором изгибающий момент на данном участке будет иметь экстремальное значение.

Подставляем значение координаты =1,0м в уравнение для  и найдем экстремальное значение изгибающего момента на данном учстке, (в нашем случае – максимум, т.к. вторая производная от  отрицательна)

По правилу “зонтика” – парабола выпуклостью вверх.

Участок №2:

(справа)

Уравнение для :

 - уравнение наклонной прямой.

Участок №3

(справа)

Уравнение для :

-уравнение наклонной прямой.

Участок №4

(справа)

Уравнение для :

-уравнение наклонной прямой.

- (шарнир “B” - справа)

Условие прочности:

Максимальный изгибающий момент с эпюры М(х):

Из условия прочности:

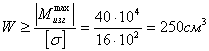
Так как профиль состоит из двух швеллеров, расчетное значение момента сопротивления уменьшаем вдвое .

Из таблицы стандартных профелей (сортамента) ГОСТ 8240-56, находим ближайшее большее к расчетному значение W=132 .

Выбираем швеллер № 18а.