Расчет различных равновесий, протекающих в природных водах, требует построения модели раствора. Такая модель должна включать константы реакций между различными компонентами раствора и метод расчета коэффициентов активности частиц в растворе. Основные равновесия макрокомпонентов природных вод приведены в Табл. 2.
Таблица 2. Равновесия макрокомпонентов в растворе (25oC, 1 Атм).
Равновесие |
lgKo |
Ссылка |
|
CO2 (газ) ó CO2 (раствор) CO2 (раствор) + H2O ó HCO3- + H+ HCO3- ó CO32- + H+ H2O ó H+ + OH- Mg2+ + CO32- ó MgCO3o Mg2+ + HCO3- ó MgHCO3+ Mg2+ + SO42- ó MgSO4o Ca2+ + CO32- ó CaCO3o Ca2+ + SO42- ó CaSO4o |
-1.47 -6.35 -10.33 -14.00 3.35 1.16 2.36 3.20 2.31 |
1 1 1 1 2 1 1 1 1 |
|
Ca2+ + CO32- ó CaCO3 (кальцит) Ca2+ + CO32- ó CaCO3 (арагонит) |
8.43 8.26 |
3 3 |
|
Mg2+ + CO32- ó MgCO3 (магнезит) Mg2+ + 2OH- ó Mg(OH)2 (брусит) |
7.52 11.15 |
4 5 |
1. Гаррелс и Крайст, 1968
2. Значение константы, приводимое Гаррелсом и Крайстом (1968) составляет 103.4; в настоящей работе эта константа уменьшена до 103.35 для лучшего согласия с экспериментальными данными по измерению валовых констант диссоциации уголекислоты в морской воде (Dickson and Millero, 1987)
3. Millero and Pierrot (1998)
4. Pokrovsky et al. (1999)
5. Baes and Messmer (1976)
Расчет коэффициентов активности в общем случае является довольно сложной задачей, однако в приближенном виде ее можно решить. В среднем, коэффициент активности иона можно описывать уравнениями (при 25оС):
pgi = -lggi = zi2D [3]
D = 0.51 · I0.5/(1+1.5 · I0.5) [4]
I = 0.5Sz2M [5]
Здесь gi, Mi и zi – коэффициент активности, моляльность (количество молей в 1 кг воды) и заряд иона, D – Дебаевский терм, I – ионная сила раствора.
Ионная сила раствора влияет также на активность нейтральных частиц. Это влияние можно описывать с помощью уравнения Сеченова:
lgγ(нейтральная частица) = ksI [6]
Здесь ks – коэффициент высаливания. Для большинства нейтральных частиц коэффициенты высаливания не известны. В настоящей работе все коэффициенты активности нейтральных частиц принимаются равными 1, за исключением углекислого газа. Коэффициент активности углекислого газа в морской воде составляет 1.162 (Millero and Pierrot, 1998). Таким образом, в работе используется следующая аппроксимация:
lgγ(CO2(p-p)) = 0.1 · I [7]
Величины ионной силы морской и речной воды (по данным Табл. 1 и 2) равны 0.67 и 0.0017 M, поэтому логарифмы средних коэффициентов активности ионов составляют, соответственно, -0.19z2 и -0.02z2. С использованием этих коэффициентов активности можно рассчитать равновесия карбонатов, которые в существенной мере определяют рН природных вод.
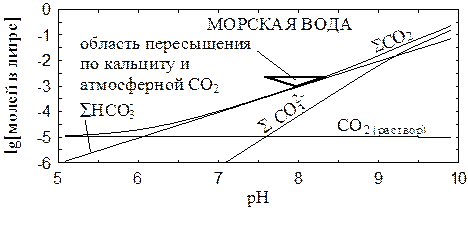
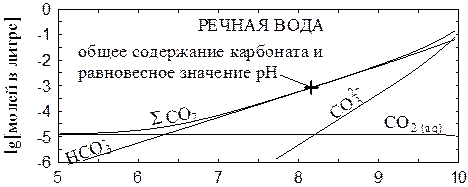
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.