Например, если ![]() ЗОО м/с,
ЗОО м/с, ![]() = l мс, λ=10 см, то М=10.
= l мс, λ=10 см, то М=10.
Потенциальная точность измерения угловых координат цели
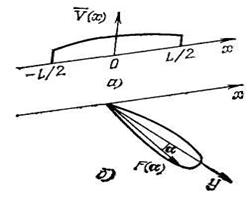
Любая цель имеет две угловые координаты: азимут и угол места. Ограничимся рассмотрением потенциальной точности измерения азимута. Она зависит от вида диаграммы направленности антенны в горизонтальной плоскости (рис. 4).
Рисунок 4.
F(α) = ![]()
![]() ,
,
где ![]() - распределение комплексных амплитуд
возбуждения антенны по её раскрыву (рис. 4а). Так как обычно используются
остронаправленные антенны, то имеет смысл в первую очередь рассмотреть
предыдущее выражение при малых α, когда sin α ≈ α
- распределение комплексных амплитуд
возбуждения антенны по её раскрыву (рис. 4а). Так как обычно используются
остронаправленные антенны, то имеет смысл в первую очередь рассмотреть
предыдущее выражение при малых α, когда sin α ≈ α
F(α) ≈ 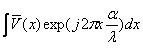
Сравнивая последнее с выражением для сигнала
![]() υ(t) =
υ(t) = ![]()
замечаем, что они полностью аналогичны и что в предыдущем выражении пространственная координата х играет роль частоты f, а величина α/λ — роль времени t.
На основании этой аналогии для минимальной дисперсии ошибки временного положения сигнала напишем аналогичное выражение для минимальной дисперсии ошибки величины а/λ
![]() ,
,
где γ – эффективная ширина раскрыва антенны.
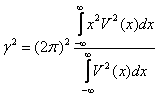 .
.
Следовательно, потенциальная точность измерения угла характеризуется величиной
![]()
Т.е ошибка измерения угла тем меньше, чем уже диаграмма направленности и чем больше отношение сигнал-шум. Относительная же угловая ошибка определяется только отношением сигнал-шум, уменьшаясь с его увеличением. Высокую разрешающую способность по углу и однозначность измерения угла обеспечивают антенны с непрерывным возбуждением её раскрыва.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.