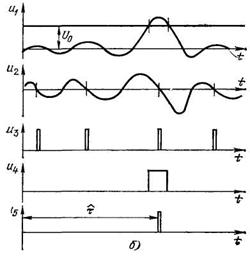
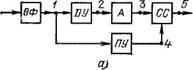
Пороговое устройство вместе с оптимальным фильтром образуют оптимальный обнаружитель, импульс обнаружения которого поступает на схему совпадения и открывает ее. При таком построении оптимального измерителя временного положения сигнала на выход схемы не проходят через схему совпадения импульсы с выхода устройства А, соответствующие максимумам шумовых выбросов (рис. 1.б). Таким образом, совмещение в одной схеме оптимального обнаружителя и оптимального измерителя временного положения сигнала позволяет устранить возможность измерения временного положения слабых шумовых выбросов.
Потенциальная точность измерения частоты
Рассматривая запись мгновенного значения простейшего
гармонического сигнала ![]() (t, f)=cos2nft, замечаем, что в ней частота
и время являются равноправными переменными. Смещенный по времени сигнал
(t, f)=cos2nft, замечаем, что в ней частота
и время являются равноправными переменными. Смещенный по времени сигнал
![]() cos2πf(t-τ)
cos2πf(t-τ)
записывается аналогично сигналу со смещением по частоте:
![]()
Эта аналогия имеет глубокий физический смысл. К тому
же точность измерения временного положения сигнала при заданном отношении
сигнал-шум определяется только основной частотной характеристикой сигнала - его
амплитудным спектром S![]() (f).
(f).
Сравнение двух приведенных выше соотношений показывает полную симметричность сигнала относительно времени и частоты. Поэтому все полученные выражения для точности измерения временного положения сигнала справедливы и при измерении частоты, если в этих выражениях поменять местами временные и частотные характеристики:
минимальная дисперсия погрешности частоты
![]() ,
,
Эффективная длительность сигнала
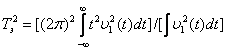
Но любой узкополосный радиосигнал можно представить в виде
![]() ,
,
где
V![]() (t) и
(t) и ![]() (t) - соответственно
законы амплитудной и фазовой модуляции этого сигнала. Поэтому получаем
(t) - соответственно
законы амплитудной и фазовой модуляции этого сигнала. Поэтому получаем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.