





1. Структурный анализ схем пространственного и сложного плоского рычажного механизма.
1.1. Начертим структурную схему пространственного рычажного механизма.
1.2. Начиная с ведущего звена, пронумеруем по порядку арабскими цифрами звенья, а буквами латинского алфавита обозначим все подвижные соединения, содержавшие в структуре механизма.
Структурная схема пространственного механизма :
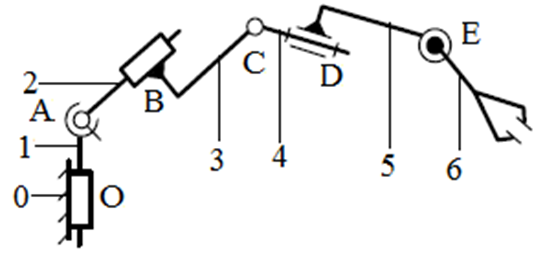
Рисунок 1.1.
Выберем структурную форму. Так как структурная схема является пространственной, то для расчетов степеней свободы будем использовать формулу Сомова-Малышева
W=6n-5![]() -4
-4![]() -3
-3![]() -2
-2![]() -
-![]() (1.1)
(1.1)
n - количество подвижных звеньев кинематической цепи,
![]() - количество кинематических пар пятого класса,
- количество кинематических пар пятого класса,
![]() - количество кинематических пар четвертого класса,
- количество кинематических пар четвертого класса,
![]() - количество кинематических пар третьего класса,
- количество кинематических пар третьего класса,
![]() - количество кинематических пар второго класса,
- количество кинематических пар второго класса,
![]() - количество кинематических пар первого класса
- количество кинематических пар первого класса
Для
определения величины коэффициента ![]() проанализируем
структурную схему механизма (рис. 1.1).
проанализируем
структурную схему механизма (рис. 1.1).
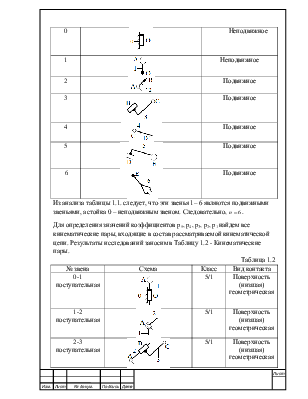
Данные представлены в виде таблицы Таблице 1.1.
Таблица 1.1.
|
№ звена |
Схема |
Кинематическое состояние |
|
0 |
|
Неподвижное |
|
1 |
|
Неподвижное |
|
2 |
|
Подвижное |
|
3 |
|
Подвижное |
|
4 |
|
Подвижное |
|
5 |
|
Подвижное |
|
6 |
|
Подвижное |
Из анализа таблицы 1.1. следует, что эти
звенья 1– 6 являются подвижными звеньями, а стойка 0 – неподвижным звеном.
Следовательно, ![]() .
.
Для определения значений коэффициентов p5, p4, p3, p2, p1 найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследований заносим в Таблицу 1.2 - Кинематические пары.
Таблица 1.2
|
№ звена |
Схема |
Класс |
Вид контакта |
||
|
0-1 поступательная |
|
5/1 |
Поверхность (низшая) геометрическая |
||
|
1-2 поступательная |
|
5/1 |
Поверхность (низшая) геометрическая |
||
|
2-3 поступательная |
|
5/1 |
Поверхность (низшая) геометрическая |
||
|
3-4 вращательная |
|
4/2 |
Поверхность (низшая) геометрическая |
||
|
4-5 вращательная |
|
5/1 |
Поверхность (низшая) геометрическая |
||
|
5-6 цилиндрическая |
|
4/2 |
Поверхность (низшая) геометрическая |
||
Из анализа данных таблицы 1.2 следует, что
исследуемый механизм состоит из четырех пар пятого класса, двух пар четвертого
класса и образует не замкнутую кинематическую цепь так, как одна из сторон
выходного звена 6 не образует кинематической пары с каким либо другим звеном. Механизм
простой. Следовательно, ![]() , а
, а ![]() .
.
Подставив найденные значения коэффициентов ![]() ,
, ![]() и
и ![]() в выражение (1.1), получим:
в выражение (1.1), получим:
![]()
Считая выходное звено неподвижным, определим маневренность пространственного рычажного механизма.
Маневренность m≥1- позволяет обеспечить работоспособность механизма
n=6-1=5
m=6*5-5*4-4*2-2*0-2*0-0=2
Результат означает, что для одного описания взаимного расположения звеньев механизмов данного вида в трехмерном пространстве при замкнутой кинематической цепи достаточно 1 обобщенной координаты.
m=W-6(const-максимальное число степеней свободы) =8-6=2
Так как условие работоспособности m≥1, следовательно, заданная структура позволит обеспечить работоспособность пространственного механизма.
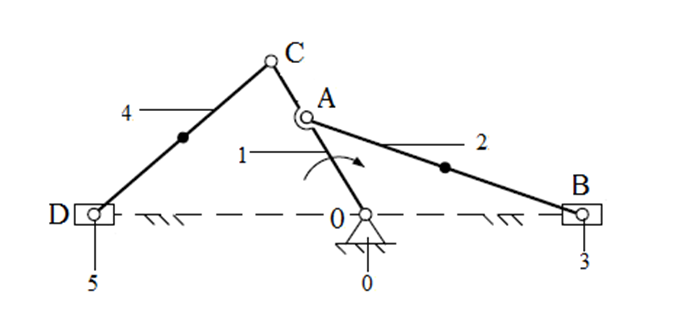
Рис. 1.2.
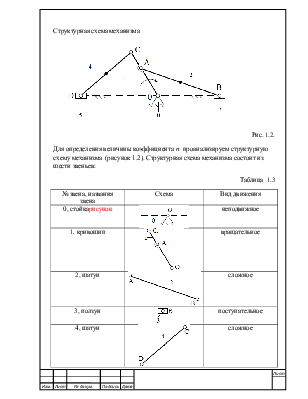
Для определения величины коэффициента ![]() проанализируем структурную схему
механизма (рисунок 1.2). Структурная схема механизма состоит из шести звеньев:
проанализируем структурную схему
механизма (рисунок 1.2). Структурная схема механизма состоит из шести звеньев:
Таблица 1.3
|
№ звена, названия звена |
Схема |
Вид движения |
|
0, стойкарисунок |
|
неподвижное |
|
1, кривошип |
|
вращательное |
|
2, шатун |
|
сложное |
|
3, ползун |
|
поступательное |
|
4, шатун |
|
сложное |
|
5, ползун |
|
поступательное |
Из анализа данных таблицы 2.2. следует, что звенья 1,2,3,4,5 - подвижны, а стойка 0- является не подвижной звеном. Следовательно, n=5
Для определения коэффициентов ![]() и
и ![]() найдем
все кинематические пары, входящие в состав рассматриваемой кинематической цепи.
Результаты исследований заносим в Таблицу 1.4
найдем
все кинематические пары, входящие в состав рассматриваемой кинематической цепи.
Результаты исследований заносим в Таблицу 1.4
Таблица 1.4
|
№ П/П |
Номера звеньев/ название |
Схема |
Класс/ подвижность |
Вид контакта/ замыкание |
|
|
1 |
0-1/ вращательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
2 |
1-2/ вращательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
3 |
2-3/ поступаетльная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
4 |
1-4/ вращательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
5 |
4-5/ поступательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
6 |
3-0/ поступательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
|
7 |
5-0/ поступательная |
|
5/1 |
Поверхность «низшая» геометрическая |
|
Из анализа данных таблицы 2.2 следует что, схема исследуемого механизма представляет собой замкнутую
кинематическую цепь, звенья которой образуют между собой семь
пар пятого класса, следовательно, ![]() =7, и не одной парой четвертого
класса
=7, и не одной парой четвертого
класса ![]() =0
=0
W = 3n
−2![]() –
–
![]() ,
,
n – число подвижных
звеньев; ![]() - число пар пятого класса;
- число пар пятого класса; ![]() - число пар четвертого класса.
- число пар четвертого класса.
W =3*5-2*7-0=15-14=1
Результат означает, что для однозначного описания взаимного расположения звеньев механизма данного вида на плоскости достаточно 1 обобщенной координаты.
Состав структуры исследуемого механизма согласно принципу построения механизмов по Ассуру.
Разобьем механизм на структурные группы Ассура, в порядке, обратном образованию механизма, начиная с выходного звена.
Группа звеньев 4-5 состоит из шатуна 4 и ползуна 5, и трех кинематических пар пятого класса: 1-4- вращательной пары и 0-5,4-5 - поступательной пары.
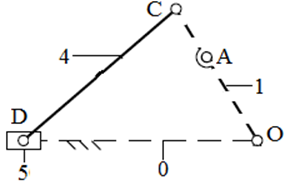
Тогда
коэффициенты формулы Чебышева принимают следующие значения: n = 2; ![]() = 3,
= 3, ![]() = 0.
= 0.
W=
3n-2![]() -
-
![]() =3*2-2*3-0=0
=3*2-2*3-0=0
Следовательно, группа звеньев 4 - 5 является группой 2 класса (так как состоит из двух звеньев и трёх пар), второго вида (так как две пары вращательные и одна поступательная) и второго типа (так как два свободных конца, которыми эта группа присоединяется к механизму).
Группа звеньев 2-3 состоит из шатуна 2 и ползуна 3, и трех кинематических пар пятого класса: 1-2- вращательной пары и 0-3, 2-3 - поступательных пар.
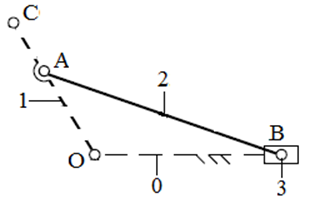
Тогда
коэффициенты формулы Чебышева принимают следующие значения: n = 2; ![]() = 3,
= 3, ![]() = 0.
= 0.
W=
3n-2![]() -
-
![]() =3*2-3*3-0=0
=3*2-3*3-0=0
Следовательно, группа звеньев 2 - 3 является группой 2 класса (так как состоит из двух звеньев и трёх пар), второго вида (так как две пары вращательные и одна поступательная) и второго типа (так как два свободных конца, которыми эта группа присоединяется к механизму).
Группа звеньев 0-1 состоит из 0- стойки и
1-кривошипа, одна кинематическая пара пятого класса, 0 - 1 -вращательная пара,
следовательно, n=1, ![]() =1,
=1,![]() =0.
=0.
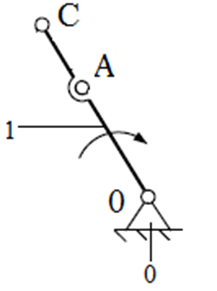
W=
3n-2![]() -
-
![]() =3*1-2*1-0=1
=3*1-2*1-0=1
Следовательно, группа звеньев 0 - 1 не является структурной группой, а представляет собой первичный механизм
Из проведенного структурного анализа следует, что структура исследуемого механизма состоит из первичного механизма с подвижностью, равной 1, и двумя структурными группами 2-го класса 2-го порядка 2-говида
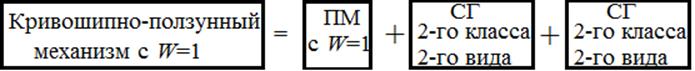
Таким образом, данный плоский рычажный механизм является механизмом 2 класса (класс механизма определяется наивысшим классом группы Ассура, входящей в данный механизм) с подвижностью равной 1.
Построение кинематической схемы выполняется в выбранном масштабном коэффициенте. Для определения масштабного коэффициента воспользуемся формулой:
µl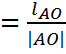
![]()
µl- масштабный коэффициент длин
lАО- длина кривошипа, м.
![]() – отрезок, изображающий длину кривошипа в принятом
масштабном
– отрезок, изображающий длину кривошипа в принятом
масштабном
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.