Структурный анализ рычажного механизма. Структурный синтез плоского рычажного механизма

Таким образом, данный плоский рычажный механизм обладает одной степенью свободы и является механизмом II класса. Класс механизма определяется наивысшим классом группы Ассура, входящей в данный механизм.

3 Структурный синтез плоского рычажного механизма

 

3.1 Кинематическая схема механизма

Построим кинематическую схему.

Рисунок 7 – Кинематическая схема

Вычислим масштабный коэффициент длины :

,                                                    

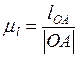где  – действительная длина кривошипа в метрах;

  – размер кривошипа в миллиметрах принимаемый на чертеже и характеризующий длину кривошипа на кинематической схеме.

.

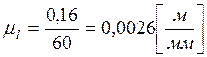Остальные размеры звеньев вычислим по формуле:

,                                                       

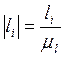где  – номер звена, для которого вычисляется длина на кинематической схеме.

,

,

,

,

.

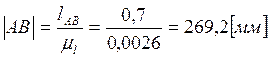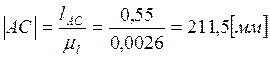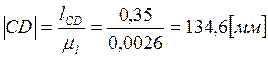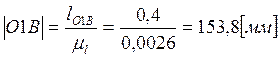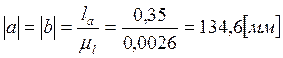Построим по заданным геометрическим параметрам кинематическую схему механизма на формате А1 в масштабном коэффициенте .

4 Кинематический анализ рычажного механизма

 

4.1 Линейные и угловые скорости точек механизма

Найдем линейные скорости точек звеньев для 12-ти положений механизма:

Рассмотрим ведущее звено (Рисунок 10) механизма:

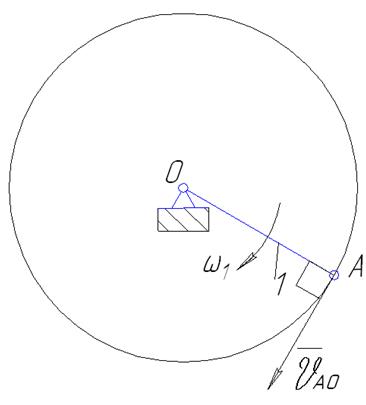
Рисунок 10

Угловую скорость первого звена найдём по формуле:

,                                       

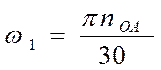где  – частота вращения первого звена.

.

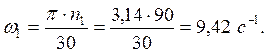При вращательном движении первого звена скорость точки А этого звена направлена перпендикулярно её радиусу вращения по направлению и равна:

 

,                                               

.

Согласно определению плоскопараллельного движения, скорость любой точки этого тела будет определяться через скорость полюса следующим образом:

,                              

,

где  – скорость точки А;

 – скорость точки О, взятой за полюс;

 – скорость вращения точки А вокруг точки О.

Зададим масштабный коэффициент скоростей :

,                                                    

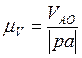где  – значение скорости вращения точки А вокруг точки О;

  – длина отрезка  на плане скоростей, представляющая скорость  на плане скоростей.

.

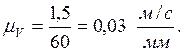
Выбираем в качестве полюса плана скоростей произвольную точку p, проводим в выбранном масштабе вектор .

Для нахождения скорости точки В рассмотрим движение второго звена, взяв за полюс точку А и  рассмотрим движение четвертого звена, взяв за полюс точку О1.

 Тогда будем иметь:

,

,

где  – неизвестная скорость точки В;

 – известная по величине и направлению скорость точки А;

 – скорость точки В при её вращении вокруг точки А, направленная перпендикулярно АВ .

 – скорость точки В при её вращении вокруг точки О1, направленная перпендикулярно О1В .

Построим план скорости для седьмого положения механизма.

Решим графически векторное равенство и найдём величины  и .

Измерив длины отрезков pb и ab и умножив их на масштабный коэффициент скоростей, в котором строится план скоростей, получим истинные значения .и .

 

,

.

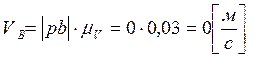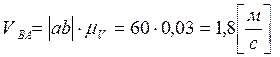Отрезок, изображающий вектор скорости точки , найдем, воспользо­вавшись теоремой подобия:

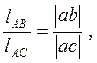
откуда

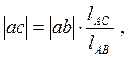
где  – длина отрезка ac на плане скоростей;

  – длина отрезка ab на плане скоростей;

  – истинная длина отрезка AС;

                 – истинная длина второго звена AB

Замерив на плане скоростей длину отрезка  и подставив найденноезначение в выражение, получим:

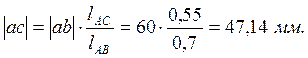
Отложим полученный отрезок ac на плане скоростей и соединив точку p с точкой c получим отрезок pc изображающий в масштабе  скорость точки С, то есть:

.

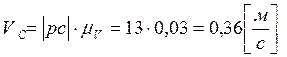Определим скорость точки D, для этого составим векторное равенство:

,                                     

,

где  – неизвестная скорость точки D;

 – известная скорость точки C;

 – скорость точки D при её вращении вокруг точки C, направленная перпендикулярно DC .

 

Решим графически векторное равенство и найдём величины  и .

Измерив длины отрезков pd и cd и умножив их на масштабный коэффициент скоростей, в котором строится план скоростей, получим истинные значения  и .

,

.

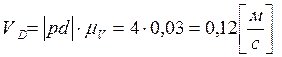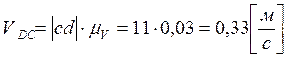Определим угловые скорости ,  и  звеньев 2, 3 и 4. Величины этих скоростей определяются из равенств:

,

.

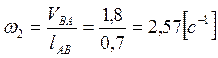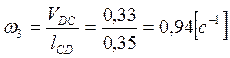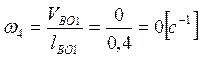
Угловые скорости ,  и  направлены в ту же сторону, куда и скорости  ,  и .

Мы нашли значения и направления линейных , , , ,  и угловых , ,  скоростей для седьмого положения механизма.

Строим планы скоростей для оставшихся положений механизма. Вычисляем истинные величины линейных и угловых скоростей для всех положений механизма и сводим их в таблицу .

Таблица 3 – Угловые и линейные скорости для двенадцати положений механизма

 

Номер положения механизма	Скорости точек,						Угловые скорости звеньев,
0	1,5	0,69	1,62	0,81	0,12	0,81	2,31	2,31	1,72
1	1,5	0,12	1,8	0,42	0,39	0,21	2,57	0,6	0,3
2	1,5	0,78	1,53	0,9	0,69	0,48	2,18	1,37	1,95
3	1,5	1,56	0,87	1,59	1,23	1,23	1,24	3,51	1,4
4	1,5	1,77	0,3	1,77	0,87	1,62	0,43	4,63	4,42
5	1,5	1,74	0,54	1,74	1,05	1,8	0,77	5,14	4,35
6	1,5	1,26	0,87	1,38	0,72	1,74	1,24	4,97	3,15
7	1,5	0	1,8	0,39	0,12	0,33	2,57	0,94	0
8	1,5	1,41	2,28	1,2	1,29	1,44	3,25	4,11	3,52
9	1,5	1,89	1,53	1,74	0,9	1,65	2,18	4,71	4,72
10	1,5	1,92	0,3	1,89	1,29	1,8	0,43	5,14	4,8
11	1,5	1,35	1,02	1,44	0,78	1,35	1,45	3,85	3,37

4.2 Линейные и угловые ускорения точек механизма

Рассмотрим сначала движение ведущего звена ОА и определим ускорение точки А. Так как кривошип ОА совершает равномерное вращательное движение (), то точка А этого кривошипа будет иметь только нормальное ускорение, равное по величине:

 

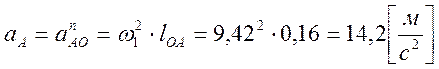
Направлено ускорение  к оси вращения О.

Масштабный коэффициент ускорений:

,                                             

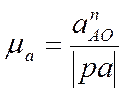где  – истинное значение нормального ускорения точки А, при вращении вокруг точки О;

  – длина отрезка pa на плане ускорений, представляющая ускорение  на плане ускорений.

.

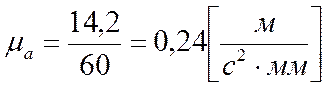Выбираем в качестве полюса плана ускорений произвольную точку p, из точки p в выбранном масштабе проведем вектор .

Рассмотрим движение второго звена.

,                                       

где  – ускорение точки В;

  – ускорение точки А;

  – ускорение точки В при её вращении вокруг точки А.

Ускорение  можно представить в виде:

,                                        

где  – нормальное ускорение точки В при её вращении вокруг точки А. Проведем расчеты угловых ускорений для седьмого положения механизма:

.

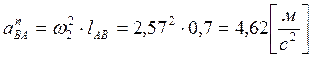 – тангенциальное ускорение точки В при её вращении вокруг точки