Определяем неизвестные реакции опор, составляя уравнение статики, страница 4

Определяем неизвестные реакции опор, составляя уравнение статики

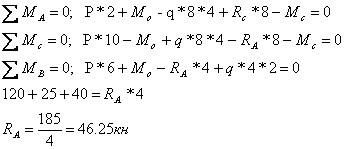
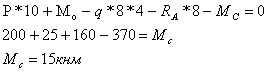
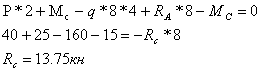
Проверка

Реакции опор определены правильно

Эпюра Q(X)

Участок №1(слева): 0£х₁£2 уравнение для Q(X₁)

Q(X₁)= -P- не зависит от х₁ – прямая параллельная оси х.

x₁=0: Q(X₁)=-P = -20 kH

x₁=2: Q(X₁)= -P= -20 kH

Участок №2(слева): 0£х₂£4 уравнение для Q(X₂)

Q(X₂)= -P+R_A-q*x₂– уравнение наклонной прямой.

х₂=0: Q(X₂)= -P+R_A =26.25kH

x₂=4: Q(X₂)= -P+R_A-q*4=6.25kH

Участок №3(справа): 0£ х₃£4 уравнение для Q(X₃)

Q(X₃)= -R_C+q* х₃ – уравнение наклонной прямой.

x₃=0: Q(X₃)=- R_С =-13.75 kH

x₃=4: Q(X₃)= R_C +q*4=6.25 kH

ЭпюраQ(X₃) пересекает ось Х , меняя знак с минуса на плюс . Найдем значение координаты х₂₀ , при котором Q(X₃)=0.

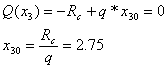
Эпюра M(X)

Участок №1(слева): 0£x₁£2: уравнение для M(X₁)

M(X₁)= -P- x₁ – уравнение наклонной прямой

x₁=0: M(X₁)= 0

x₁=2: M(X₁)= -P* 2= -40 kHм

Участок №2(слева): 0£x₂£4 уравнение для M(X₂)

M(X₂)= -P(x₂+2)-Mo+R_A*x₂-q* x₂* x₂/2– уравнение параболы.

x₂=0: M(X₂)= -P*2- Mo =-65 kH

x₂=4: M(X₂)= -P*6- Mo +R_A* 4-q*4*2= 0 kHм

Участок №3(справа): 0£х₃£4 уравнение для M(X₃)

M(X₃)= - MC +R_C*x₃ –q* x_3* x_3/2– уравнение параболы

x₃=0: M(X₃)= - MC =-15 kHм

x₃=4: M(X₃)= - MC +R_C* 4-q*4*2 =0 kHм

Для нахождения третьей точки параболы воспользуемся дифференциальной зависимостью.

Вычислим производную от M(x₁), приравняем к нулю и найдем координату х₁₀, при которой изгибающий момент на данном участке имеет экстремальное значение

Условие прочности

Максимальный изгибающий момент с эпюры M(X)

Из условия прочности

Так как профиль состоит из двух швеллеров, то расчётное значение уменьшаем вдвое: W=203см³, из таблицы стандартных профилей находим ближайшее большее к расчетному значение W =212см³, выбираем швеллер № 22A.