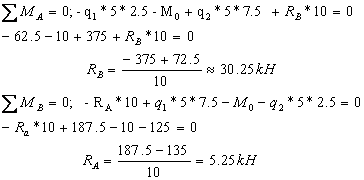
Проверка:
![]()
Реакции опор определены правильно
Эпюра Q(x)
Участок №1(слева): 0£x1£5 уравнение для Q(x1)
Q(x1)=RA-q1*x1 – уравнение наклонной прямой
x1=0: Q(x1)= RA=5.25 kH
x1=5: Q(x1)=RA-q1*5= 5.25-25= - 19.15 kH
Эпюра Q(x1) пересекает ось x1, меняя знак плюса на минус. Найдем координату x10. Вычислим координату x0, при которой Q(x1)=0
Q(x0)=Ra-q1*x10=0, x10=Ra/q1=1.0м
Участок №2(справа): 0£х2£5 уравнение для Q(x2)
Q(x2)= RB –q*x2– уравнение наклонной прямой.
х2=0: Q(x2)= RB= 30.25kH
x2=4: Q(x2)= RB-q2*5= -19.75 kH
Эпюра Q(x2) пересекает ось x, меняя знак с плюса на минус, найдём координату x20, при которой Q(x2)=0
Q(x20)=RB-q2*x20=0 x20=RB/q2=30.25/q2=3.0м
Эпюра M(X)
Участок №1(слева): 0£x1£5: уравнение для M(x1)
M(x1)=RA*x1-q* x1*x1/2 – уравнение параболы.
Для построения этой параболы найдем три ее точки :
x1=0: M(x1)=0
x1=5: M(x1)=RA*5- q*5*2.5 = 5.25*5-5.5*2.5= - 36.25 kHм
Для нахождения третьей точки параболы воспользуемся дифференциальной зависимостью.
![]()
Вычислим производную от M(x1), приравняем к нулю и найдем координату х10, при которой изгибающий момент на данном участке имеет экстремальное значение
![]() x10=Ra/q1=1.0м
x10=Ra/q1=1.0м
Найдём значение изгибающегося момента на данном участке (в нашем случае – максимум, т.к. вторая производная от M(x1) – отрицательна).
![]()
Участок №2(справа): 0£х2£5 уравнение для М(x2).
M(x2)=-RB*x2+q2*x2*x2/2 – уравнение параболы.
Для построения этой параболы найдём три её точки.
х2=0: M(x2)=0
x2=5: M(x2)= -RB*5+q2*5*2.5=-30.25*5+10*5*2.5=-26.25 kHм
Для нахождения третьей точки параболы воспользуемся дифференциальной зависимостью.
![]()
Вычислим производную от M(x2), приравняем к нулю и найдем координату х20, при которой изгибающий момент на данном участке имеет экстремальное значение
![]() x10=Ra/q2=3.0м
x10=Ra/q2=3.0м
Найдём экстремальное значение изгибающегося момента (в нашем случае – минимум, т.к. вторая производная от M(x2) – положительна).
![]()
Условие прочности
![]()
Максимальный изгибающий момент с эпюры M(x)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.