Определяем неизвестные реакции опор, составляя уравнение статики, страница 3

Момент сопротивления для круглого сечения: , h/b=2, h=2b: W=2b³/3

Из условия прочности

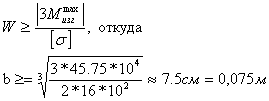
Дано:

q=5H/м

P=20 kH

М=15 kHм

[s]=160 Мпа=1600кг/см²

Определяем неизвестные реакции опор, составляя уравнение статики

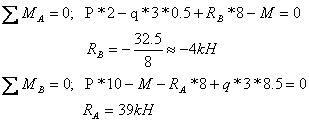
Проверка

Реакции опор определены правильно

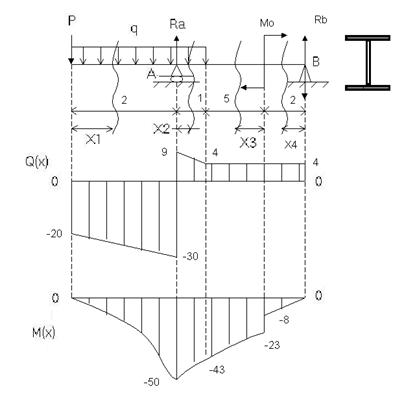
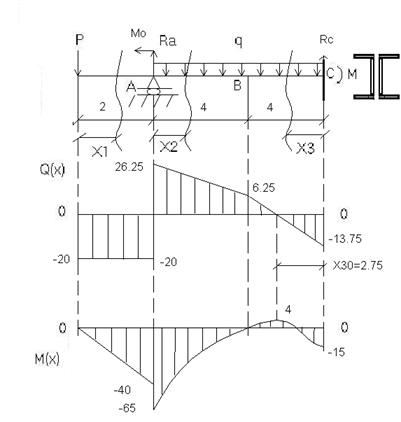
Эпюра Q(X)

Участок №1(слева): 0£х₁£2 уравнение для Q(X₁)

Q(X₁)= q*х₁- уравнение наклонной прямой

x₁=0: Q(X₁)=-P=-20 kH

x₁=2: Q(X₁)= -P-q*2= -30 kH

Участок №2(слева): 0£х₂£1 уравнение для Q(X₂)

Q(X₂)= -P-q*2+R_A-q*x₂– уравнение наклонной прямой.

х₂=0: Q(X₂)= -P-q*2+R_A =-9kH

x₂=1: Q(X₂)= -P-q*2+R_A-q*1=4kH

Участок №3(справа): 0£х₃£2 уравнение для Q(X₃)

Q(X₃)= R_B– не зависит от х₃ – прямая параллельная оси х.

x₃=0: Q(X₃)= R_B =4 kH

x₃=2: Q(X₃)= R_B =4 kH

Участок №4(справа): 0£х₄£5 уравнение для Q(X₄)

Q(X₄)= R_B – прямая параллельная оси х.

x₄=0: Q(X₄)= R_B =4 kH

x₄=5: Q(X₄)= R_B =4 kH

Эпюра M(X)

Участок №1(слева): 0£x₁£2: уравнение для M(X₁)

M(X₁)= -P* x₁-q* x_1* x₁/2 – уравнение параболы

x₁=0: M(X₁)= 0

x₁=2: M(X₁)= -P* 2-q*2* 1 = -50 kHм

Участок №2(слева): 0£x₂£1 уравнение для M(X₂)

M(X₂)= -P(x₂+2)-q*2(x₂+1)+R_A*x₂-q* x₂* x₂/2– уравнение наклонной прямой

x₂=0: M(X₂)= -P*2-q*2*1=-50 kH

x₂=1: M(X₂)= -P*3=q*2*2+R_A*1-q*1*0.5= -43 kHм

Участок №3(справа): 0£х₃£2 уравнение для M(X₃)

M(X₃)= -R_B*x₃ – уравнение наклонной прямой

x₃=0: M(X₃)= 0

x₃=2: M(X₃)= -R_B*2=-8 kHм

Участок №4(справа): 0£х₄£5 уравнение для Q(X₄)

Q(X₄)= - R_B*(x₄+2)-M – наклонная прямая.

x₄=0: Q(X₄)= R_B*2-M= -23 kH

x₄=5: Q(X₄)= R_B*7-M= -43 kH

Условие прочности

Максимальный изгибающий момент с эпюры M(X)

Из условия прочности

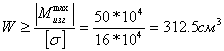
Выбираем двутавр № 24A.

Дано:

q=5кH/м

P=20 kH

М=25 kHм

[s]=160 Мпа=1600кг/см²