 Дано:
Дано:
q=5 kH/м
P1=10 kH
P2= 10 kH
[s]=160 Мпа=1600кг/см2
Т.к. эпюра представляет из себя замещение (заделку), то реакций этой опоры можно не определять. Они получаться автоматически при построении эпюр перезывающих и изгибающих моментов.
Правило знаков при построении эпюр.
Перезывающая сила
Слева: (+), (-)
Справа: (+), (-)
Изгибающий момент
Слева: (+), (-)
Справа: (+), (-)
Будем осуществлять обход участков по длине балки – справа.
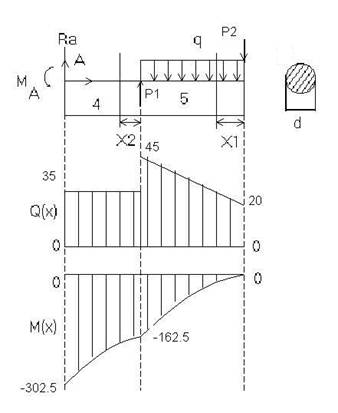
Эпюра Q(X)
Участок №1(справа): 0£х1£5 : уравнение для Q(X1)
Т.к. на длинном участке поперечные силы отсутствубт, то уравнение для перезывающих сил на этом участке будет представлять из себя уравнение оси X. Q(x1)=0
Участок №2: уравнение для Q(X2) 0<x2<4
Q(x2)= P+q*x2 - уравнение наклонной прямой
х2=0: Q(x2)= P=10 kH
x2=4: Q(x2)= P +4*q =10+5*4=30 kH
Участок №3: 0<x3<3. Уравнение для Q(x3)
Q(x3)=p+q*4 – не зависит от x3 – прямая параллельная оси X.
x3=0: Q(x3)=30kH
x3=3: Q(x3)=30kH
Проверка: ![]() 30-20-10=0
30-20-10=0
Эпюра M(X)
Участок №1: (справа) 0£x1£2: уравнение для M(x1)
M(x1)=M0 - не зависит от x1 – прямая параллельная оси X.
x1=0: M(x1)=M0=10kHм
x1=2: M(x1)= M0=10kHм
Участок №2: (справа) 0£x2£4 уравнение для M(x2)
M(x2)=M0 - P2 *x2 - q*x2 *x2/2 – уравнение параболы.
x2=4: M(x2)= M0- P*4 - q*4*2 =-10-40-40= - 70 kHм
x2=0: M(x2)= M0=10 kHм
Участок №3: 0£x3£3 уравнение для M(x3)
M(x3)=M0 – P1 (x3 + 4)-q*4 *(x3+2) – уравнение наклонной прямой.
x3=0: M(x3)= M0- P*4 - q*4*2 = - 70 kHм
x3=0: M(x3)= M0=-P*7-q*4*5=10-70-100= -160 kHм
Проверка: ![]() Ma-q*4*5-P*7+M0=0
Ma-q*4*5-P*7+M0=0
160-100-70+10=0
Условие прочности
![]()
Максимальный изгибающий момент с эпюры M(x)
![]()
Момент сопротивления для
круглого сечения: ![]()
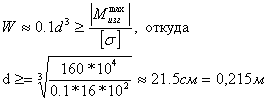
Задача №2.
Дано:
q=5 kH/м
P=10 kH
M=10 kHм
[s]=160 Мпа=1600кг/см2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.