где ![]() – объем выборки, ед.;
– объем выборки, ед.;
![]() - i-ый член вариационного ряда.
- i-ый член вариационного ряда.
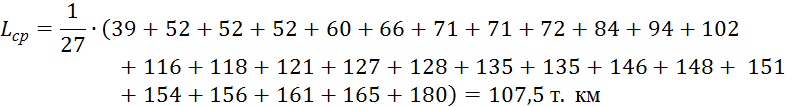
Дисперсия (несмещенная) точечной оценки наработки до отказа:
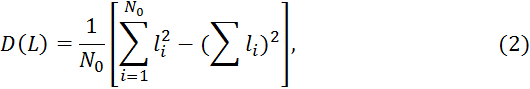
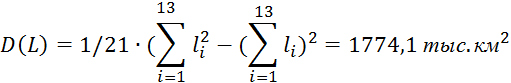
Среднее квадратическое отклонение:
![]()
![]()
Коэффициент вариации точечной оценки средней наработки до отказа:

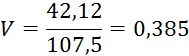
Определим параметр формы b закона Вейбула-Гнеденко, он принимается в зависимости от коэффициента вариации по таблице, находящейся в методическом указании:
![]()
Расчетное значение предельной относительной ошибки:
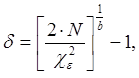 (5)
(5)
где ε-
уровень значимости, следовательно ![]() (42)=28,14, это значение
выбираем из таблицы значения квантилей
(42)=28,14, это значение
выбираем из таблицы значения квантилей ![]() -
распределения.
-
распределения.
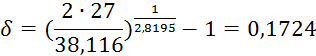
Нижняя и верхняя границы данного интервала следующие:
![]()
![]()
![]()
![]()
Это означает, что действительное значение средней наработки до отказа находится в интервале [90,6; 128,35] км.с вероятностью 0,9.
Оценка параметра масштаба закона Вейбулла-Гнеденко:
Точечная оценка параметра масштаба “а” закона Вейбулла-Гнеденко:

где 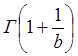 - гамма функция.
- гамма функция.
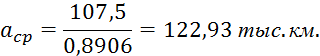
Граничные значения интервальной оценки:
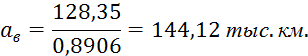
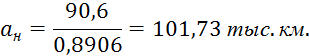
Прежде чем перейти к оценке остальных показателей надежности, необходимо проверить принятую нами нулевую гипотезу о соответствии экспериментального распределения отказов распределению Вейбулла-Гнеденко или Нормальному закону.
Проверка нулевой гипотезы:
Соответствие закона Вейбула-Гнеденко экспериментальному распределению проверяем по c2 - критерию согласию Пирсона.
Нет основания для отклонения от нулевой гипотезы при соблюдении условия:
![]()
Где![]() - значение критерия Пирсона,
вычисленное по экспериментальным данным;
- значение критерия Пирсона,
вычисленное по экспериментальным данным;
![]() - критическая точка (табличное значение)
критерия Пирсона при уровне значимости
- критическая точка (табличное значение)
критерия Пирсона при уровне значимости ![]() и числе степеней свободы
и числе степеней свободы![]() ;
;
![]() - уровень значимости;
- уровень значимости;
![]() - число степеней свободы.
- число степеней свободы.
Нулевая гипотеза проверим по следующему алгоритму:
1. Рассчитать количество
интервалов ![]() по правилу Штюргеса с округлением до целого значения:
по правилу Штюргеса с округлением до целого значения:
![]()
![]()
Разделим на ![]() интервалов размах вариационного
ряда, т.е. разность между наибольшим и наименьшим числами.
интервалов размах вариационного
ряда, т.е. разность между наибольшим и наименьшим числами.
Границы интервала найдем по формуле:

где ![]() - номера интервалов;
- номера интервалов;
![]() – максимальное значение вариационного ряда, тыс.км;
– максимальное значение вариационного ряда, тыс.км;
![]() – минимальное значение вариационного ряда, тыс.км.
– минимальное значение вариационного ряда, тыс.км.
Таблица1 – Расчет эмпирических частот
|
j |
Lj |
Lj+1 |
nj |
nj² |
∆F(Lj+1) |
n*j |
nj²/n*j |
|
1 |
0 |
63,51 |
5 |
25 |
0,143888 |
3,884976 |
6,435046 |
|
2 |
63,51 |
88,02 |
5 |
25 |
0,3229 |
4,833323 |
5,172425 |
|
3 |
88,02 |
112,54 |
2 |
4 |
0,541367 |
5,8986 |
0,678127 |
|
4 |
112,54 |
137,05 |
7 |
49 |
0,743004 |
5,44421 |
9,000387 |
|
5 |
137,05 |
161,56 |
6 |
36 |
0,884765 |
3,827558 |
9,405475 |
|
6 |
161,56 |
∞ |
2 |
4 |
1 |
3,111332 |
1,285623 |
2. Исходя из нулевой гипотезы, рассчитаем теоретические частоты по формуле:
![]()
Где![]() - вероятность отказа для
- вероятность отказа для ![]() члена;
члена;
![]() - вероятность отказа для
- вероятность отказа для ![]() члена.
члена.
Функцию распределения отказов, входящую в формулу (12), определим по формуле:
Для закона Вейбулла-Гнеденко:
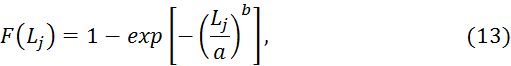
Расчет n*J произведем табличным способом.
3. Определить расчетное значение критерия Пирсона

Для закона Вейбулла-Гнеденко:
![]()
![]()
Определим число степеней свободы:
![]()
где ![]() - количество параметров
предполагаемого распределения.
- количество параметров
предполагаемого распределения.
для закона Вейбулла-Гнеденкоr =1:
![]()
Значит, ![]() :
:
![]()
Гипотеза
выполняется, так как![]() .
.
Оценка вероятности безотказной работы:
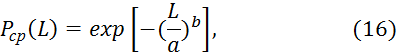
где ![]() - вероятность безотказной работы (точечная оценка).
- вероятность безотказной работы (точечная оценка).
Интервальную оценку ![]() определим при подстановке в формулу (16)
вместо
определим при подстановке в формулу (16)
вместо ![]() значения
значения ![]() и
и ![]() .
.
Таблица 2 – Точечная оценка вероятности безотказной работы до первого отказа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.