Определение момента инерции симметричного тела

Работа 8. определение момента инерции симметричного тела

Цель работы - определить момент инерции сим­метричного тела.

Общие сведения

Момент инерции тела  является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент  инерции  тела   зависит  от   распределения  массы  тела относительно оси вращения . Для вычисления момента инерции твердого тела относительно данной оси  разобьем мысленно тело на большое число весьма малых элементов - материальных точек . Тогда момент инерции тела

или

,

где Dm_i - масса элемента; r_i - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.

            В данной работе для определения момента инерции тела используется метод крутильных колебаний.

Если тело, висящее на нерастяжимой нити (так, что направление нити проходит через центр тяжести тела), повернуть в горизонтальной плоскости на некоторый угол a, то в результате деформации нити возникнет упругая сила. Она создаст крутящий момент (момент силы) М , возвращающий систему в исходное состояние. В результате возникнут крутильные колебания.

Известно, что при небольших отклонениях от равновесия момент М пропорционален углу a. Введя коэффициент пропорциональности D - модуль кручения, зависящий от упругих свойств нити, получим

М = -Da.

Если пренебречь силами сопротивления, то основной закон динамики вращательного движения можно записать в виде

М = -Da = Je .          (1)

Учитывая, что

уравнение (1) можно привести к виду

.        (2)

Решением уравнения (2) являются функции синуса или косинуса

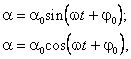
(здесь  - амплитудное значение угла отклонения; w - круговая частота;  - начальная фаза), дифференцируя которые два раза по времени, получим

.       (3)

Уравнение (3) тождественно уравнению (2), если

.         (4)

Так как , где T - период колебаний, то уравнение (4) можно записать в виде

.           (5)

            Из этой формулы можно найти момент инерции тела по измеренному периоду колебаний.

В измерениях используют установку, состоящую из трехкулачкового патрона, подвешенного к нижнему концу тонкой упругой проволоки, верхний конец которой закреплен во втулке, соединенной с рычагом пускового механизма. Вся система вертикально прикреплена к штативу с помощью специального кронштейна. Измеряется период колебаний патрона, патрона и сплошного цилиндра и патрона и исследуемого тела.

Пусть J_о - момент инерции патрона; J₁ - момент инерции сплошного цилиндра; J_х - момент инерции испытуемого тела. Тогда

  (6)

где Т₀ - период колебаний патрона; Т₁ - период колебаний патрона и сплошного цилиндра; Т_х - период колебаний патрона и исследуемого тела; D - модуль кручения.