Из уравнений (6), исключив D и J0, можно получить
![]() (7)
(7)
Момент инерции сплошного цилиндра
![]() (8)
(8)
где m и R - масса и радиус цилиндра, m = rV; r - плотность материала цилиндра, r = 7,7×103 кг/м3; V - его объем, V = pR2h; h - высота цилиндра.
Таким образом,
![]() (9)
(9)
Более
точно момент инерции цилиндра можно определить, если учесть момент инерции
держателя ![]() . Однако
. Однако ![]() << J, поэтому
<< J, поэтому ![]() можно пренебречь.
можно пренебречь.
Порядок выполнения работы
Перед началом измерений необходимо убедиться в правильности установки прибора по уровню. Работая с прибором, следует соблюдать следующие правила: проволоку нельзя сгибать, растягивать и т.п.; нельзя допускать на приборе колебания подвеса с большой амплитудой (угол отклонения системы от положения равновесия не должен превышать 10°).
Последовательность проведения измерений следующая:
1) придерживая кулачковый патрон, чтобы он не пришел в колебательное движение, правой рукой сблизить рычаги пускового механизма (пластинчатая пружина "защелкивается" за выступ, проволока приводится в состояние покоя);
2) нажав на конец пластинчатой пружины, ввести в действие пусковой механизм, вызывающий крутильные колебания патрона;
3) определить с помощью секундомера время 50 полных колебаний системы t0 и найти период колебаний Т0 = t0/50. Повторить опыт несколько раз;
4) аналогично определить периоды колебаний патрона с цилиндром (Т1) и с исследуемым телом (Тх);
5) измерить диаметр цилиндра и по формуле (9) рассчитать момент инерции J1.
Результаты измерений оформить в виде таблицы:
|
Номер опыта |
m |
T0 |
T1 |
Tx |
Jx |
Вычислив средние значения Т0, Т1 и Тх, по формуле (2) рассчитать момент инерции Jx.
Так
как на установке проводятся многократные измерения, то целесообразно вычислить
среднее квадратическое отклонение ![]() Удобно сначала
рассчитать относительную погрешность
Удобно сначала
рассчитать относительную погрешность ![]() а затем
а затем ![]() . На основании формул теории
погрешности можно получить (необходимо уметь выводить это соотношение)
. На основании формул теории
погрешности можно получить (необходимо уметь выводить это соотношение)
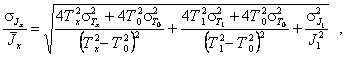
где ![]() ,
, ![]() и
и
![]() - средние квадратические отклонения Тх,
Т0 и Т1,
- средние квадратические отклонения Тх,
Т0 и Т1, 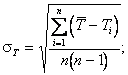
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.