Практически важное значение имеет среднее во времени значение потока энергии через единицу площади, движущегося от источника звука:
|
|
Это среднее во времени значение называется интенсивностью звука. Интенсивность звука есть среднее количество звуковой энергии, проходящей в единицу времени через единицу поверхности, перпендикулярной к направлению распространения звуковой волны. В системе СИ единицей интенсивности является ватт на метр квадратный (Вт/м2).
При синусоидальных колебаниях с круговой частотой![]()
![]() Определяя согласно (2.12) интенсивность звука за период колебания Т, находим
Определяя согласно (2.12) интенсивность звука за период колебания Т, находим
|
|
где Рзвэ и г>э — эффективные значения звукового давления и колебательной скорости. Для сферической волны с учетом выражения (2.11) имеем
|
|
(2.15)
В поле сферических звуковых волн в результате их расхождения интенсивность звука убывает с удалением от источника. Однако средний поток энергии через сферическую поверхность с радиусом га (рис. 2.6) вследствие малых потерь энергии в среде будет таким же, как и через любую другую поверхность с большим радиусом г\, (если в промежутке между ними нет поглотителей энергии или других источников). Отсюда мощность звуковой волны ,
![]()
где 1а и /J — интенсивности звука для поверхностей с радиусами га и rj. Из выражения (2.16) следует квадратичный закон убывания интенсивности звука в сферической волне:
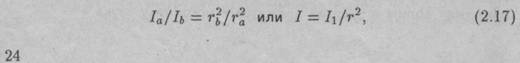
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.