Линейные характеристики звукового поля, страница 5

На расстоянии г от излучателя звуковое давление в каждой точке сферической поверхности может быть представлено в виде

(2.6)

где рзв! — амплитуда звукового давления на расстоянии 1 м от цен­тра сферы.

Как видно из выражения (2.6), амплитуда звукового давления р-₃вт уменьшается с увеличением расстояния от центра источника звука. Под­ставляя (2.6) в уравнение движения среды и интегрируя по времени, имеем

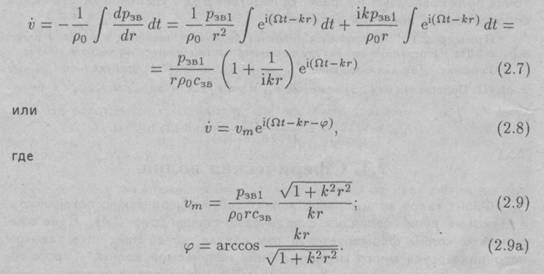
Из выражений (2.6) и (2.7) определим акустическое сопротивле­ние для сферической волны

где b — (fcr²/[I + (kr)²} и х = kr/[l+ (kr)²} — безразмерные коэффи­циенты, зависящие от длины волны и расстояния между источником звука и точкой наблюдения.

Модуль акустического сопротивления

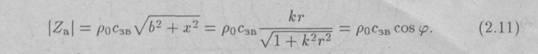
Из (2.9) и (2.11) видно, что между скоростью колебания и звуко­вым давлением существует фазовый сдвиг </?. На рис. 2.5 изображена зависимость угла у? (в градусах) от отношения расстояния от центра источника сферической волны до точки наблюдения к длине волны.

22

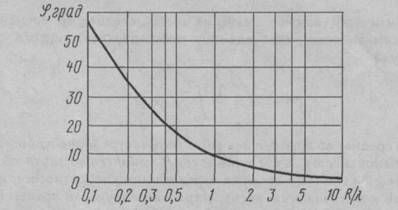
Рис. 2.5. Фазовый сдвиг между звуковым давлением и колебательной скоростью в сферической волне

Из рисунка видно, что на расстояниях, превышающих длины волны (Я/А > 10), фазовый сдвиг между р_зв и v настолько мал, что фронт волны в направлении звукового луча можно считать плоским и поль­зоваться выражением (2.5).

Пример 2.2. Амплитуда звукового давления сферической волны на расстоя­нии 1 м от точечного источника p₃»i = 8 Па. Определить амплитуду колебательной скорости на расстоянии 10 м от источника звука с частотой 1000 Гц и фазовый сдвиг V? между звуковым давлением и колебательной скоростью.

Решение. Из выражения (2.9а) следует, что фазовый сдвиг

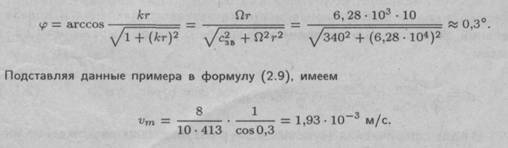
2.5. Энергетические характеристики звукового поля

В бегущей звуковой волне поток энергии определяется вектором Умова:

U = p_3Bv.

Если в рассматриваемой точке звукового поля мгновенное значение р_зв и vимеют одинаковый знак, то вектор Умова направлен в сторону распространения звуковой волны, т.е. энергия движется от источника звука. Если они имеют разные знаки, то вектор Умова направлен против движения волны и энергия движется к источнику звука.

23