Линейные характеристики звукового поля, страница 2

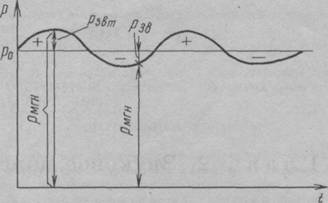
Рис. 2.1. Изменение звукового давления в точке звукового поля при излучении синусоидальной волны

ременная. В момент сжатия оно положительно: р_мгн > ро. ^в момент разряжения отрицательно: р_мгн < ро (рис. 2.1).

Звуковое давление измеряют в Паскалях. Давление в один паскаль (Па) создается при действии силы в один ньютон (Н) на поверхность площадью в один квадратный метр: Па = Н/м². Паскаль в 10⁵ меньше атмосферного давления. В акустике имеют дело со звуковым давле­нием, не превышающим 100 Па.

Скорость распространения звуковой волны в воздухе (скорость зву­ка) с_зв в основном зависит от метеорологических условий и температу­ры! Однако с точностью, достаточной для технических расчетов, можно считатьгде Т — абсолютная температура воздуха, К.

При нормальном атмосферном давлении и температуре Т — 290 К (17 °С) скорость звука с_зв = 340 м/с. Это значение с_зв использует­ся в технических расчетах.

Колебательное движение частиц среды при распространении зву­ковой волны характеризуется также колебательным смещением от по­ложения покоя, которое происходит с определенной скоростью, назы­ваемой колебательной:

где t/_CM — смещение частиц.

Не следует путать эту скорость со скоростью звука с_зв. Скорость звука величина постоянная для данной ср'еды и зависит от метеороло­гических условий и температуры воздуха Колебательная скорость на несколько порядков меньше с_зв и возрастает при увеличении частоты и амплитуды акустического сигнала. Колебательную скорость считают по­ложительной, если частицы среды смещаются в направлении движения волны, и отрицательной, если эти движения встречны. Колебательная скорость измеряется в метрах в секунду (м/с).

18

Если источник звука совершает колебания по гармоническому зако­ну с частотой F, то за время Т, в течение которого совершается один период колебания источника, фронт звуковой волны переместится на расстояние, равное длине волны А. За 1 с волна распространяется на расстояние, численно равное скорости звука г_зв = F\.

2.2. Связь между звуковым давлением и колебательной скоростью

Выделим в звуковом поле элементарный объем воздуха, заключен­ный между боковыми поверхностями Д5, находящимися на расстоянии Дг друг от друга и перпендикулярными к направлению звуковых лучей (рис. 2.2). Масса воздуха в выделенном объеме ДгДб" равна />оДгД5", где pq — плотность среды.

Среда в рассматриваемом объеме находится под действием разности давлений р_зв и р_зв + Др_зв. Следовательно, сила, под действием которой может происходить движение этого объема воздуха,

Если под действием приложенной силы ДрзвДб" элементарный объ­ем воздуха с массой po&rASприобретает ускорение dv/dt, то по вто­рому закону Ньютона сила инерции

Так как р_зв ^и vзависит как от координат, так и от времени, то, перейдя к частным производным, после несложных преобразований по­лучим

 '     (2.1) Данное уравнение называют уравнением движения среды.