Определение коэффициента магнитосопротивления, исследование зависимости подвижности носителей заряда от температуры, страница 7

4. Определить удельную проводимость образца в отсутствии магнитного поля:

σ₀=ℓ/(R₀S),

где S=d·x=10^-5 м², ℓ=0,02 м.

5. Определить холловскую подвижность μ_H основных носителей заряда и ее дисперсию s_μH при комнатной температуре:

μ_H=R_H·σ₀,

6. По данным табл.3 построить зависимость холловского напряжения U_H от абсолютной температуры. По наличию смены знака U_H определить тип основных носителей заряда. Найти температуру перекомпенсации.

7. По данным табл.5 рассчитать и построить зависимость логарифма проводимости ln(σ) от обратной температуры 1/T:

σ=1/ρ=(I·x)/(U_обр·d·ℓ),

где I=30 мА, d=10^-3 м, ℓ=0,02 м,  x=0,01 м.

 

По наклону графика определить ширину запрещенной зоны E_g образца:

E_g=2k·tg(β),

где k – постоянная Больцмана.

8. Этот пункт выполняется только в случае образцов n-типа. Рассчитать и построить зависимость холловской подвижности от температуры:

μ_H=R_H·σ

Сравнить с зависимостью μ_H ~ T^-3/2., соответствующей рассеянию носителей заряда на колебаниях кристаллической решетки.

9. По данным табл.4 рассчитать сопротивление образца в присутствии магнитного поля R_В=U_обр/I. Построить график зависимости относительного изменения сопротивления |(R_B-R₀)/R₀| от B².

 

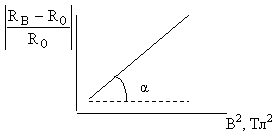По наклону линии найти коэффициент магнитосопротивления:  К=tg(α).