Определение коэффициента магнитосопротивления, исследование зависимости подвижности носителей заряда от температуры, страница 2

С учетом того, что скорость носителя заряда v может быть выражена через плотность тока j как v=j/(qp), где p – концентрация положительных носителей заряда, получим для напряжения Холла

                                                         (3)

Здесь через R_H обозначена величина 1/(qp), которая носит название постоянной Холла. Как видно напряжение Холла U_H прямо пропорционально току I и индукции магнитного поля В. Из этого выражения, зная величину постоянной Холла  и величину положительного заряда, можно найти концентрацию носителей заряда

Если ток создается отрицательными носителями заряда, то их скорость направлена против технического направления тока. В выражении (1) одновременно со знаком заряда меняет знак и скорость, поэтому направление силы Лоренца не изменяется. Отрицательные заряды будут также отклоняться к передней грани. Это означает, что полярность напряжения Холла изменится. Постоянная Холла будет равна

,                                                              (4)

где q – абсолютная величина отрицательного заряда, n – концентрация отрицательных носителей заряда. Как видно, знаки постоянной Холла для положительных и отрицательных носителей заряда оказываются противоположными. Таким образом, по полярности напряжения Холла можно определять тип носителей заряда.

2. Подвижность носителей заряда.

Дрейфовая скорость движения носителей заряда зависит от величины электрического поля Е и от свойств материала

v=μE,                                                                        (5)

где μ учитывает свойства материала и называется подвижностью. Подвижность определенная в эффекте Холла называется холловской подвижностью и обозначается μ_H. С учетом этого соотношения условие стационарности тока в эксперименте по эффекту Холла можно записать как

                                                         (6)

Так как поле, обеспечивающее ток I, равно E=U_обр/x (U_обр – падение напряжения на образце, x – толщина образца), то холловская подвижность равна

                                                                     (7)

С другой стороны, используя U_обр = IR, где  I – ток через образец, а R = ρx/(ℓd) – сопротивление образца, получим

.                                                  (8)

Здесь ρ – удельное сопротивление образца, σ – удельная проводимость образца.

Таким образом, определить подвижность носителей заряда в образце можно зная R_H и удельную проводимость σ или U_H, U_обр, В и геометрические размеры образца.

3. Зависимость напряжения Холла от температуры.

При повышении температуры изменяются как концентрация свободных носителей заряда, так и их подвижность. Это приводит к зависимости U_H от температуры. Зависимость концентрации свободных носителей заряда от температуры описана в разделе «Зонная структура» и имеет вид:

примесная

                                              (9)

собственная

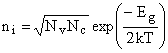,                                                   (10)

где Е_акт – энергия активации (ионизации) примесей, E_g – ширина запрещенной зоны, N_V, N_C – плотность энергетических состояний в валентной зоне и проводимости соответственно, N_пр – концентрация примесей, k –постоянная Больцмана.