Планирование оборота розничной торговли и товарных запасов: Пособие для проведения семинарских, практических занятий и самостоятельной работы по курсу «Планирование на предприятии (в торговле)», страница 3

Теснота взаимосвязи показателей измеряется с помощью коэффициента корреляции (r):

где x, y –фактическое значение переменных; n – число слагаемых.

Упростим формулу, изменив точку отсчета одной из переменных на среднее значение (). Тогда каждое новое значение будет равно , но алгебраическая сумма отклонений фактических значений x от его среднего значения равна нулю .

В результате преобразований формула коэффициента корреляции принимает вид:

Полученный коэффициент корреляции можно оценить по табл. 1.2

Таблица 1.2

Качественная оценка тесноты связи, шкала Чеддока [28. C. 8]

В процессе анализа кроме оценки тесноты связи, можно определить степень воздействия исследуемого признака на тот или иной параметр через коэффициент детерминации (). Коэффициент детерминации показывает количественное влияние какого-либо фактора на исследуемый признак.

II этап – выбирают математическое уравнение, отражающее эту зависимость.

III этап – находят параметры данного уравнения.

IV этап – проводят прогнозирование (теоретическое, выровненное) оборота розничной торговли на основе выбранного уравнения.

V этап – проводят оценку достоверности (погрешности) полученных плановых значений показателя.

Сравнивая расчетный (выравненный) оборот розничной торговли с фактическим за каждый год исследуемого периода, можно сделать вывод о том, что полученная модель развития оборота розничной торговли точно описывает реальный процесс. Окончательный вывод о возможности использования полученной экономико-математической модели развития оборота розничной торговли для его прогнозирования на планируемый период можно сделать, дав количественную оценку ошибки (отклонения) прогноза от его возможного развития .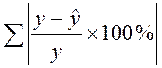

Ошибка является незначительной (от 1-7 %), что позволяет использовать полученную модель для прогнозирования объема оборота розничной торговли на планируемый год. В уравнение регрессии следуеь вместо t подставить цифру, следующую по порядку в динамическом ряду.

Чаще всего в практике планирования оборота розничной торговли  используется линейная модель прогноза общего объема оборота розничной торговли:

где у – планируемый объем оборота розничной торговли, тыс. руб.; t – годы по порядку; a₀, a₁ – коэффициенты уравнения регрессии, определяемые по способу наименьших квадратов.

Параметры a₀, a₁ можно определить, решив следующую систему уравнений:

Для решения подобной системы уравнений необходимо уравнять коэффициенты при одном из двух неизвестных (a₀ или a₁). Для этого либо обе части первого уравнения умножают на , а обе части второго уравнения – на n; либо обе части первого уравнения делят на n, а обе части второго уравнения – на.

Кроме однофакторных моделей планирования оборота розничной торговли, наиболее распространенными являются многофакторные линейные модели [26]:

а также однофакторные и многофакторные уравнения параболы 2-го и более высоких порядков:

где y – планируемый объем оборота розничной торговли, тыс. руб.; t – фактор времени; a₀, a₁, a₂ – параметры уравнения, определяемые путем решения системы трех уравнений с тремя неизвестными; x_1, x₂ – факторы, оказывающие влияние на оборот розничной торговли.

При решении многофакторных показательных и экспоненциальных моделей обычно производят их преобразование (через логарифмирование) к линейному виду.

Параметры a₀, a₁, a₂ можно определить, решив следующую систему уравнений:

Подставив в уравнение значение t, получим прогнозируемое значение (теоретическое, выравненное) оборота розничной торговли для всего динамического ряда, если степень достоверности расчетов соответствует требованиям, рассчитываем общий объем оборота розничной торговли  на планируемый год.