I. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ.
Необходимыми условиями правильности утверждения А называются такие условия, без соблюдения которых утверждение А заведомо не может быть верным.
Достаточными условиями правильности утверждения А называют условия, при которых утверждение А заведомо верно.
Приведем три примера.
1. Необходимым условием делимости целого числа N на 4 без остатка является четность числа N. Условие это необходимо, но не достаточно. Иначе говоря, если число N не является четным, оно не может делиться без остатка на 4, но если число N является четным, то это число может делиться на 4, а может и не делиться.
2. Достаточным условием того, что D АВС – равнобедренный, является условие равносторонности D АВС. Это условие достаточно: если D АВС равносторонний, то он заведомо равнобедренный, но не является необходимым, D АВС может быть равнобедренным, не будучи равносторонним.
3. Необходимым и достаточным условием того, что D АВС – прямоугольный является равенство а2+b2=с2, где а, b, с – длины сторон D АВС, причем с – длина наибольшей стороны.
Из определений необходимого и достаточного условий следует:
1. Если для правильности утверждения А необходимо утверждение В, то для правильности утверждения В достаточно утверждения А.
2. Если для правильности утверждения А достаточно утверждения В, то для правильности утверждения В необходимо утверждение А.
3. Если для правильности утверждения А необходимо утверждение В, то из того, что утверждение А верно, следует, что верно утверждение В: (А®В), и из того, что утверждение В неверно (ùВ), следует, что А также неверно (ùА): (ùВ®ùА).
4. Если для правильности утверждения А достаточно утверждения В, то из того, что утверждение В верно, следует, что верно утверждение А: (В®А), и из того, что утверждение А неверно следует, что и В – неверно: (ùА®ùВ).
5. Если для правильности утверждения А необходимо и достаточно утверждения В, то утверждения А и В тождественны, то есть (А«В), (ùА«ùВ), (АºВ).
Рассмотрим необходимое и достаточное условия принадлежности объекта к какому-то множеству.
] А Ì В, то есть множество А является подмножеством множества В. Тогда верны следующие утверждения (тождественные между собой):
1. Для того чтобы хÎВ, достаточно, чтобы хÎА (если хÎА, то хÎВ).
2. Для того чтобы хÎА, необходимо, чтобы хÎВ (опять, хÎА, то хÎВ). 3. Для того чтобы хÏВ необходимо, чтобы хÏА (если хÏВ, то хÏА).
4. Для того чтобы хÏА, достаточно, чтобы хÏВ (опять, если хÏВ, то хÏА).
Верно и обратное: если выполнено любое из четырех утверждений, то А Ì В.
Запишем условие "если хÎА, то хÎВ" в виде "из А следует В" или "А®В". Понятно, что А можно назвать причиной, В – следствием. Следствие "шире" причины.
Часто при формулировке каких-то условий вместо терминов "необходимо" и "достаточно" используются термины "только тогда" и "тогда".
Тождественными являются утверждения:
"для А необходимо В"
"А выполнено только тогда, когда выполнено В"
"если А, то В"
"из А следует В"
"если ùВ, то ùА"
"из отсутствия В следует отсутствие А"
"для В достаточно А"
"В выполнено тогда, когда выполнено А"
Заучивать наизусть материал этого параграфа не рекомендуется. Надо сопоставить написанное выше с элементарными понятиями русского языка, составить простые примеры для себя лично, и в случае необходимости восстановить в памяти приведенный здесь материал.
Разберем несколько примеров.
Четырех угольник называется ромбом, если все его стороны равны.
Четырех угольник называется квадратом, если все его стороны равны, и все его углы – прямые.
Обозначим через А – множество всех квадратов, через В – множество всех ромбов. Очевидно, А Ì В (А есть подмножество В). Следовательно, можно сказать:
- для того чтобы четырехугольник был квадратом, необходимо, чтобы он был ромбом;
- для того чтобы четырехугольник был ромбом, достаточно, чтобы он был квадратом;
- если четырехугольник есть квадрат, то он есть ромб;
- если четырехугольник не есть ромб, то он не является квадратом.
2. Известно, что бабушка ходит в кино только на комедии.
Следовательно, можно сказать:
- для того чтобы бабушка пошла в кино, необходимо, чтобы там демонстрировали комедию;
- достаточным признаком того, что в зале демонстрируется комедия, является присутствие бабушки;
- если бабушка пошла в кино, то там демонстрируется комедия (но если бабушка не пошла в кино, то там может демонстрироваться что угодно, и комедия, и не комедия);
- если в кинотеатре не идет комедия, то там нет бабушки (но если в кинотеатре идет комедия, то бабушка может, как присутствовать, так и отсутствовать в зале).
2.. ПРОЦЕНТЫ. ФОРМУЛА СЛОЖНЫХ ПРОЦЕНТОВ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.
Напомним, что процентом числа S называется сотая часть этого числа.
( 1% от S ) = 0,01 S
( 25% от S ) = 0,25 S
( 80% от S ) = 0,8 S
( 213% от S ) = 2,13 S
( g% от S ) = ![]()
Следует запомнить:
При увеличении числа S на g % получим 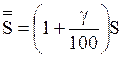 .
.
При уменьшении числа S на g % получим 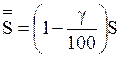 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.