Необходимые и достаточные условия. Проценты. Формула сложных процентов и второй замечательный предел, страница 2

Если 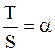,    то       Т составляет (100a)% от S,   но

S составляет ()% от Т.

Когда употребляют фразу: "Т меньше S на g %" или "Т больше S на g %", то 1% считают равным 0,01 S, т.е. 1% берется от того числа, которое называют последним.

Поэтому, фраза "Т больше S на g %" не означает, что S меньше Т на те же g %. Ясно, что Т  больше  S  на величину  ,  S меньше на  Т  на ту же величину  , но в первом случае   Т   больше   S   на 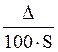    %, а во  втором случае

S   меньше   Т   на %.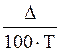

Рассмотрим пример:

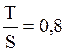;          Т=0,8S;                      S=1,25Т.

Число Т меньше S на 20%, так как

Т составляет 80% от S и за 100% принимается S.

Число S больше Т на 25%, так как

S составляет 125% от Т и за 100% принимаетсяТ.

Получается, что если какую-то величину уменьшили на 20%, то для получения ее снова уменьшенный результат надо увеличить не на 20%, а на 25%.

В том случае, когда используют термин "процент", обязательно указывается, явно или неявно, от какой именно величины процент берется.

Рассмотрим задачу:

Число S увеличили на 20%. Результат на 20% уменьшили, получили число Q. Найти отношение чисел S и Q.

Решение: Очевидно, что S¹Q, так как число S увеличивают на 20% от числа S, а полученный результат (обозначим его Р) уменьшают на 20% от этого результата, который не равен S. Учтем, что 20% от любого числа Т равны 0,2Т, тогда

Р=(1+0,2)S=1,2S

Q=(1-0,2)P=0,8P=0,8×1,2S=0,96S

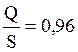
Ответ:   , конечный результат Q составляет 96% от S.

Комментарий к задаче:

Если в какой-то организации зарплату увеличили на 20%, затем на 20% уменьшили, то зарплата не стала равной первоначальной, а упала по сравнению с ней на 4%.

В общем случае, при увеличении S на g%, а затем уменьшении результата на g%, конечный результат Q будет составлять 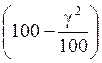% от S, то есть упадет на 0,01g²%.

.

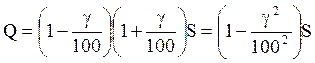То же самое получится, если S уменьшить на g%, а результат на  g% увеличить.

Рассмотрим еще одну задачу, связанную с вычислениями процентов от вклада в банк. Задача эта любопытна тем, что в ее решении используется второй замечательный предел

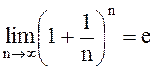,   где е=2,71823.

В банк положена сумма S. Годовой доход составляет g%. Условия вклада позволяют снять деньги со счета раньше, чем через год, получив не g%, а соответственно меньше: 0,5g% за полгода, 0,25g% за три месяца и т.п.

Все операции проводятся бесплатно. Вкладчик n раз в год посещает банк, снимает всю сумму плюс % от нее, и новую увеличенную сумму опять кладет в банк.

Требуется ответить на следующие вопросы:

            1. Какой процент дохода получит вкладчик к концу года, если будет посещать банк каждые полгода? каждые три месяца? каждую неделю?

2. Какой максимальный процент годового дохода можно получить, посещая банк как можно чаще, например, ежедневно?

Решение:

Введем обозначения:

Р=0,01g; S - сумма, положенная в банк первоначально.

Если вкладчик посещает банк каждые полгода (n=2), то через полгода он получит сумму, равную

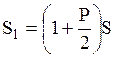, через год

.

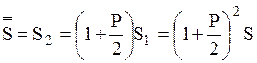Годовой доход по абсолютной величине равен 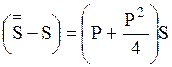, что составляет

.

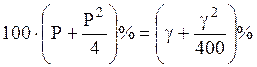При n=2 будет получено не g% дохода, а 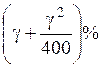 (если g=20%, годовой доход составит 21%, если g=3%, годовой доход составит  3,0225%).

Если вкладчик посещает банк каждые три месяца (n=4), то через три месяца он получит

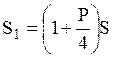, через полгода

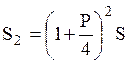, через девять месяцев

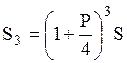, через год

.

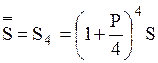При n=4 будет получено не g% дохода, а .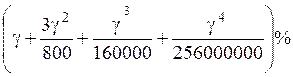

(Если g=20%, годовой доход составит 21,550%, если g=3%, годовой доход составит 3,034%.)

При посещении банка каждую неделю (n=52), в конце года будет получена сумма

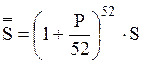     (напомним:  Р=0,01g;   S - сумма, положенная в банк первоначально.).

(Если g=20%, годовой доход составит 22,0934279%, если g=3%, годовой  доход составит 3,044562%.)

Максимальный годовой доход (при n®¥) рассчитаем следующим образом:

Сумма , полученная вкладчиком в конце года,

.

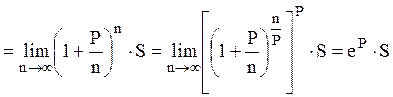Абсолютный годовой доход будет равен

, что составляет %.

(Если g=20%, годовой доход составит 22,1409%, если g=3%, годовой доход составит 3,045%.)

Заметим, что при g=100%, то есть при объявленном удвоении "неподвижного" вклада за год, реальный доход можно довести до , что составляет 171,828% (на 71,828% больше указанного).

Составим таблицу.

Таблица показывает, что, обещая клиентам g% годового дохода и не ограничивая операции с вкладами, банк на самом деле может быть вынужден выплатить более высокий процент. Дополнительный процент растет вместе с  g  по закону, проиллюстрированному таблицей. При малых процентных ставках разница не является существенной, но при g=10% она доходит до 0,5%, а при g=50% составляет уже 14,872%, что нельзя оставлять без внимания.