Элементы линейной алгебры. Матрицы. Типы матриц. Действия с матрицами. Ранг матрицы. Системы линейных уравнений

3.  ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.

3.1 Матрицы. Типы матриц. Действия с матрицами.

Матрицей называют прямоугольную таблицу чисел

,

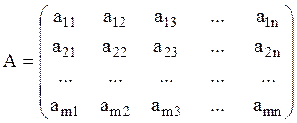- число, стоящее в i-той строке и j-том столбце.

Размерностью матрицы А называют количество ее строк и столбцов. Записывают размерность матрицы как индекс:  - матрица, имеющая m строк и n столбцов.

Условие равенства матриц: равенство размерностей и всех соответствующих элементов

.

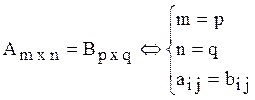Типы матриц:

1. Матрица-столбец:   .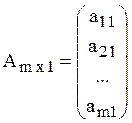

2. Матрица-строка:   .

3. Ступенчатая матрица: каждая строка матрицы кроме, может быть, первой начинается с нуля; в начале каждой следующей строки нулей больше, чем в предыдущей.

Например:      .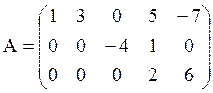

4. Квадратная матрица:  матрица, у которой количество строк равно количеству столбцов.

В квадратной матрице элементы называют элементами главной диагонали. 

Среди квадратных матриц выделяют

- симметричные (относительно главной диагонали): .

Например:       .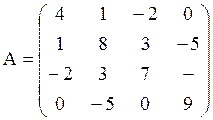

- верхние треугольные (нули ниже главной диагонали):    для всех   i>j.

Например:     .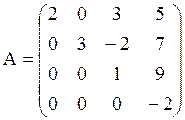

- нижние треугольные ((нули выше главной диагонали):      для всех    i<j.

Например:   .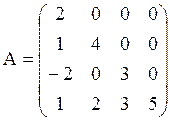

- диагональные:  для всех   i¹j.

Например: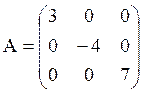    

- единичные, которая традиционно обозначается Е (или I, реже). .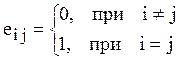

Например: .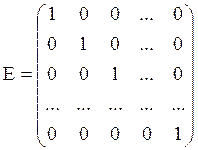

Действия с матрицами:

1. Транспонирование:         В=А^Т   Û   

Например: .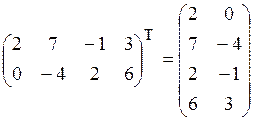

2. Умножение на число      В=aА   Û   .

3. Сложение двух матриц (операция имеет смысл только для матриц одной размерности)     Û    /

4. Умножение двух матриц (операция имеет смысл только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы)  Û 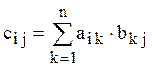. (или проще:  )

Например: .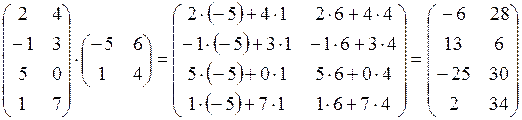

Справедливо следующее:

1)

2)  

3)

4) А×В¹В×А (как правило). (если А×В=В×А, то А и В называют взаимно перестановочными)

5) А×(В+С)=АВ+АС

6) (АВ)×С=А×(ВС)

3.2 Определитель квадратной матрицы. Схема Гаусса вычисления определителей.

Каждой квадратной матрице ставится в соответствие число, вычисленное по определенному правилу. Число это называют "определитель матрицы" и обозначают чаще всего D, det А или 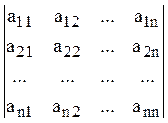 (матрицу заключают в круглые скобки; замена скобок на "палки" означает, что имеется в виду не матрица, а ее определитель).

Сформулируем правило вычисления определителя, которое не является его определением, а только следует из определения. Строгое определение определителя матрицы здесь  приводить не будем.

Пусть 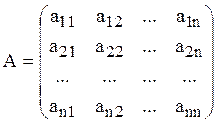     ,    тогда

,                    (*)

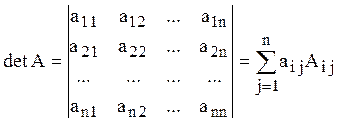где i – номер произвольно выбранной строки (ответ на зависит от выбора i, это доказывается);

В приведенной формуле :

 - алгебраическое дополнение элемента

 – минор элемента ,  т.е. определитель остатка матрицы А после вычеркивания i-ой строки и j-ого столбца.

Равенство (*) сводит вычисление определителя n–ого порядка (порядком определителя матрицы называют количество строк и столбцов этой матрицы) к вычислению определителя порядка .

Определитель второго порядка вычисляется по формуле: .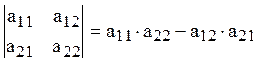

Следовательно, можно при вычислении определителя порядка n перейти к порядку , затем , и т.д. до определителей второго порядка.

Пример 1:

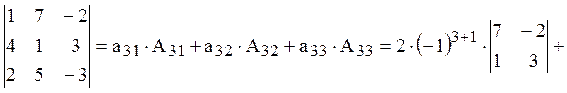
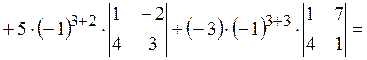
(при вычислении была выбрана третья строка).

Пример 2.

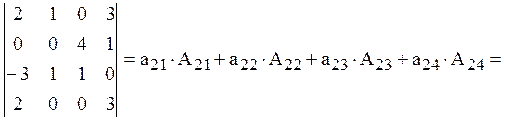
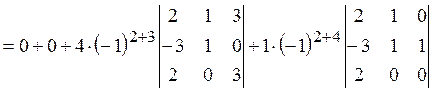
Вычислим два определителя третьего порядка:

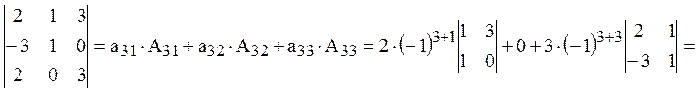
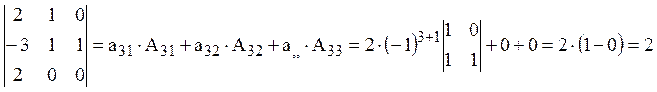
В итоге:

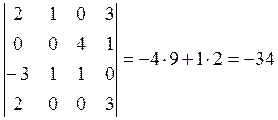
Легко заметить, что для вычисления одного определителя порядка n предложенный алгоритм может потребовать вычисления n×(n-1)×(n-2)× ×...×4×3 определителей второго порядка. (при n=10, например, 1814400 определителя) Поэтому на практике определители вычисляются по схеме Гаусса. Эта схема позволяет, используя свойства определителей, преобразовать матрицу определителя к треугольной, верхней или нижней, не меняя значения определителя. Определитель же верхней или нижней треугольной матрицы равен произведению диагональных элементов.

Свойства определителей:

1. det A=-det А^Т (в силу этого все дальнейшие свойства, формулируемые для строк верны и для столбцов)

2. Если определитель содержит строку, целиком состоящую из нулей, то он равен нулю.

3. Если определитель содержит две равные или пропорциональные строки, то он равен нулю.

4. Если в определителе поменять местами две любые строки, определитель сменит знак.

5. Если элементы одной из строк определителя умножить на какое-то число, определитель умножится на то же число.

6. Величина определителя не изменится, если к элементам одной из строк