Домашнее индивидуальное задание. № 1-2 (для всех направлений подготовки)
1. Даны две матрицы А и В:
А = 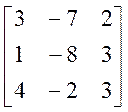 , В =
, В = 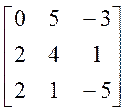
Найдите: 1.1) 3А-9А, 1.2 ) АВ, 1.3) ВА, 1.4) А-1 , 1.5) А2.
1.1. 3А-9А.
3А = 3 × 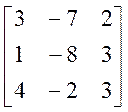 =
= 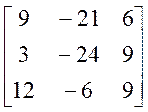
9А = 9 × 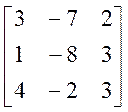 =
= 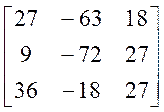
3A – 9A = 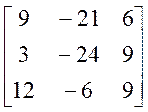 -
- 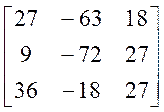 =
= 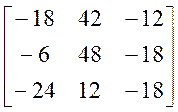
1.2. АВ.
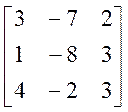 ×
×
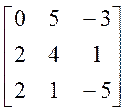 =
= 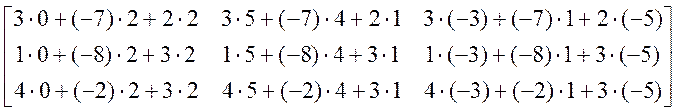 =
= 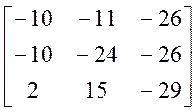
1.3. ВА.
В × А = 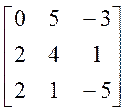 ×
× 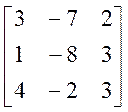 =
=
= 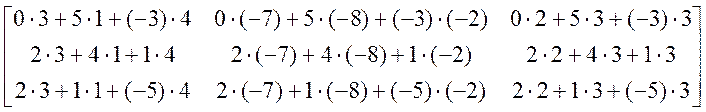 =
= 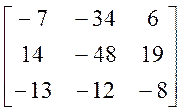
Комментарий:
Обратите внимание на тот факт, что АВ ![]() ВА
ВА
1.4. А-1.
А11 = (-1)1+1 × М11 = (-1)1+1 × 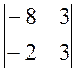 = (-8×3 – (-2)×3) = -18
= (-8×3 – (-2)×3) = -18
А12 = (-1)1+2 × М12 = (-1)1+2 × 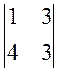 = (-1) × (1×3 - 4×3) = 9
= (-1) × (1×3 - 4×3) = 9
А13 = (-1)1+3 × М13 = (-1)1+3 × 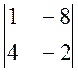 = (-2×1 – 4×(-8)) = 30
= (-2×1 – 4×(-8)) = 30
А21 = (-1)2+1 × М21 = (-1)2+1 × 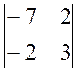 = (-1) × (-7×3 – (-2)×2) = -17
= (-1) × (-7×3 – (-2)×2) = -17
А22 = (-1)2+2 × М22 = (-1)2+2 × 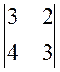 = (3×3 - 4×2) = 1
= (3×3 - 4×2) = 1
А23 = (-1)2+3 × М23 = (-1)2+3 × 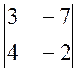 = (-1) × (3×(-2) - 4×(-7)) = 22
= (-1) × (3×(-2) - 4×(-7)) = 22
А31 = (-1)3+1 × М31 = (-1)3+1 × 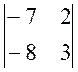 = (-7×3 – (-8)×2) = -5
= (-7×3 – (-8)×2) = -5
А32 = (-1)3+2 × М32 = (-1)3+2 × 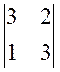 = (-1) × (3×3 - 2×1) = -7
= (-1) × (3×3 - 2×1) = -7
А33 = (-1)3+3 × М33 = (-1)3+3 × 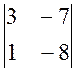 = (3×(-8) - 1×(-7)) = -17
= (3×(-8) - 1×(-7)) = -17
D = 3 × (-1)1+1 × 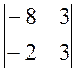 + (-7) × (-1)1+2 ×
+ (-7) × (-1)1+2 × 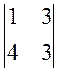 + 2 × (-1)1+2 ×
+ 2 × (-1)1+2 × 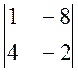 = 3 × (-24 + 6) + 7 × (3 - 12) – 2 × (-2 + 32) = -177
= 3 × (-24 + 6) + 7 × (3 - 12) – 2 × (-2 + 32) = -177
А-1
= ![]()
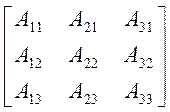 =
-
=
- ![]()
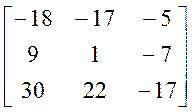
1.5. А2.
А2
= А × А = 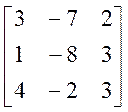 ×
× 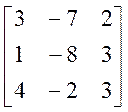 =
=
= 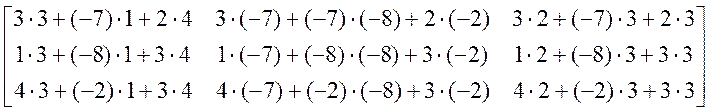 =
= 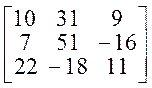
2.
Вычислить определитель D: 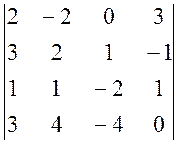 .
.
Разложим определитель по элементам первой строки:
D = 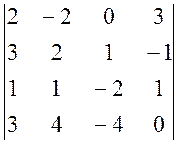 = a11
× A11 + a12 × A12 + a13 × A13 + a14 × A14. Теперь вычислим A11, A12,
A13, A14,
также разлагая соответствующие
определители по элементам первой строки.
= a11
× A11 + a12 × A12 + a13 × A13 + a14 × A14. Теперь вычислим A11, A12,
A13, A14,
также разлагая соответствующие
определители по элементам первой строки.
A11 = (-1)1+1 × M11 = 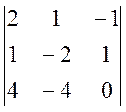 = 2 × (-1)1+1 ×
= 2 × (-1)1+1 × 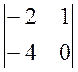 + 1 × (-1)1+2 ×
+ 1 × (-1)1+2 × 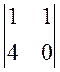 + (-1) × (-1)1+3 ×
+ (-1) × (-1)1+3 ×  =
=
= 2 × (0 + 4) – (0 - 4) – (-4 + 8) = 8
A12 = (-1)1+2 × M12 = -1 × 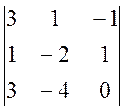 =
=
= -1 × 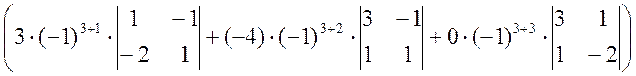 =
=
= -1 × (3 × (1 - 2) + 4 × (3 + 1)) = -13
A13 = (-1)1+3 × M13 = 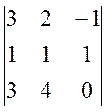 =
=
Так как a13 = 0, произведение a13 × A13 = 0, A13 считать не нужно
A14 = (-1)1+4 × M14 =  =
-1 ×
=
-1 × 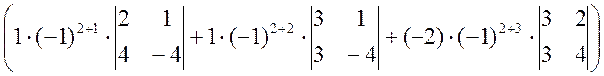 =
=
= -1 × ( -1 × (-8 - 4) + (-12 - 3) + 2 × (12 - 6) ) = -9
D= 2 × 8 + (-2) × (-13) - 3 × 9 = 16 + 26 + 27 = 15
Комментарий:
При вычислении определителей разумно сначала преобразовать определитель, используя свойства определителя таким образом, чтобы в какой-то строке (столбце) определителя все элементы кроме одного были бы равны 0. А затем получившийся определитель разложить по элементам упомянутой строки (столбца). Вычислим таким образом заданный определитель
D = 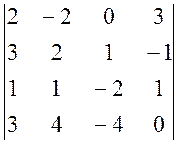 . Добьемся
того, что бы в 3-й строчке определителя все элементы, кроме a31
были бы равны 0.
. Добьемся
того, что бы в 3-й строчке определителя все элементы, кроме a31
были бы равны 0.
С этой целью:
1.
Из 2-ого столбца определителя вычтем первый столбец. Величина
определителя при этом не изменится: D = 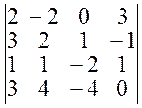 =
=  .
.
2. Умножим в преобразованном определителе 1-й столбец на (-2) и сложим полученный результат с 3-им столбцом. Величина определителя при этом не изменится:
D = 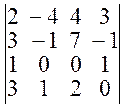 .
.
3. Умножим в преобразованном определителе 1-й столбец на (-1) и сложим полученный результат с 4-ым столбцом. Величина определителя при этом не изменится:
D = 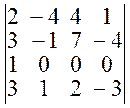 .
.
4. Полученный определитель разложим по элементам 3-й строки:
D =![]()
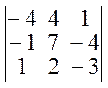 =(добиваемся
того, чтобы в 3-ей строчке все элементы кроме a21 были=0) =
=(добиваемся
того, чтобы в 3-ей строчке все элементы кроме a21 были=0) = 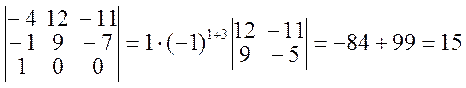 .
.
3. Проверьте совместимость системы уравнений и, в случае совместности, решите ее: 1) используя правило Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.
 .
.
Пусть A = 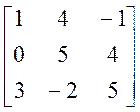 , B =
, B =  ,
, 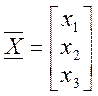 . Тогда заданная
система записывается так:
. Тогда заданная
система записывается так: ![]() .
.
3.1. Проверка системы на совместность.
A = 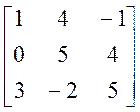 B =
B =  .
Находим определитель системы:
.
Находим определитель системы:
D = 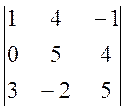 =
0 × (-1)2+1 ×
=
0 × (-1)2+1 ×  +
5 × (-1)2+2 ×
+
5 × (-1)2+2 × 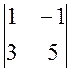 +
4 × (-1)2+3 ×
+
4 × (-1)2+3 × 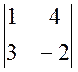 =
5 × (5 + 3) – 4 × (-2 - 12) =
96
=
5 × (5 + 3) – 4 × (-2 - 12) =
96
D ¹ 0 , следовательно, система совместна и имеет единственное решение.
3.2. Решение с использованием правила Крамера.
Находим побочные определители D1, D2, D3:
D1 = 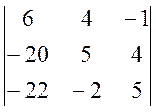 D2 =
D2 = 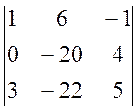 D3 =
D3 = 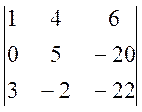 . И тогда:
. И тогда:
D1 = 6 × (-1)1+1 × 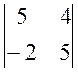 +
4 × (-1)1+2 ×
+
4 × (-1)1+2 × 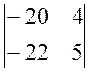 +
(-1) × (-1)1+3 ×
+
(-1) × (-1)1+3 × 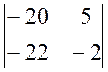 =
6 × (25 + 8) – 4 × (-100 + 88) – (40 + 110) = 96
=
6 × (25 + 8) – 4 × (-100 + 88) – (40 + 110) = 96
D2 = 0 × (-1)2+1 × 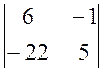 +
(-20) × (-1)2+2 ×
+
(-20) × (-1)2+2 × 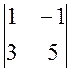 +
4 × (-1)2+3 ×
+
4 × (-1)2+3 ×  =
-20 × (5 + 3) – 4 × (-22 - 18) =
0
=
-20 × (5 + 3) – 4 × (-22 - 18) =
0
D3 = 0 × (-1)2+1 × 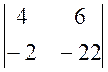 +
5 × (-1)2+2 ×
+
5 × (-1)2+2 ×  +
(-20) × (-1)2+3 ×
+
(-20) × (-1)2+3 × 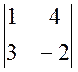 =
5 × (-22 - 18) + 20 × (-2 - 12) = -480
=
5 × (-22 - 18) + 20 × (-2 - 12) = -480
И тогда . поскольку
x1 = ![]() x2 =
x2 = ![]() x3 =
x3 = ![]() ,
получаем ответ:
,
получаем ответ:
x1 = ![]() =
1 x2 =
0 x3 =
=
1 x2 =
0 x3 =  = -5, или
= -5, или
X = 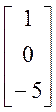
3.3. Решение с помощью обратной матрицы.
Пусть A-1 обратная
к матрице А, тогда решение системы запишем в виде ![]() .Найдем обратную матрицу A-1. Они находятся из соотношения:
.Найдем обратную матрицу A-1. Они находятся из соотношения:
А-1
= ![]()
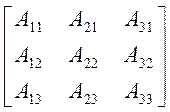 . Находим последовательно
. Находим последовательно![]() :
:
A11 = (-1)1+1 × M11 = 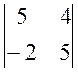 = 25 + 8 = 33
= 25 + 8 = 33
A12 = (-1)1+2 × M12 = (-1) × 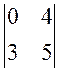 = -1 × (0 – 12) = 12
= -1 × (0 – 12) = 12
A13 = (-1)1+3 × M13 = 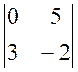 =
0 - 15 = -15
=
0 - 15 = -15
A21 = (-1)2+1 × M21 = -1 ×  = -1 × (20 - 2) = -18
= -1 × (20 - 2) = -18
A22 = (-1)2+2 × M22 = 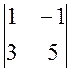 =
5 + 3 = 8
=
5 + 3 = 8
A23 = (-1)2+3 × M23 = (-1) × 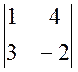 = -1 × (-2 -12) = 14
= -1 × (-2 -12) = 14
A31 = (-1)3+1 × M31 = 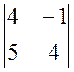 = 16 + 5 = 21
= 16 + 5 = 21
A32 = (-1)3+2 × M32 = -1 × 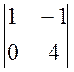 =
-4
=
-4
A33 = (-1)3+3 × M33 = 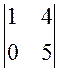 = 5, и следовательно
= 5, и следовательно
A-1 = ![]()
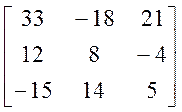 B =
B =  , но тогда
, но тогда
X = ![]()
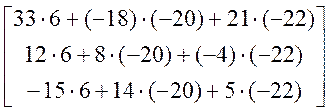 =
=
![]()
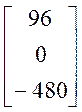 =
=

3.4. Решение методом Гаусса.
 .
.
Преобразуем расширенную матрицу системы (прямой ход).
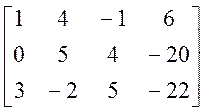 ®
® 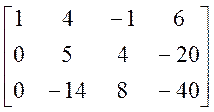 ®
® 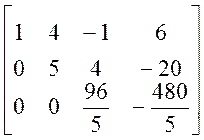 .
.
Полученная в результате преобразования матрица
есть матрица системы, равносильной исходной 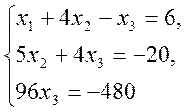 ,
и тогда (обратный ход)
,
и тогда (обратный ход)
x3 = -5
5x2 + 4 × (-5) = -20
5x2 = 0
x2 = 0
x1 + 4 × 0 – (-5) = 6
x1 = 1, или
X
= 
4. Проверьте совместимость системы уравнений, вычисляя ранги матрицы системы и расширенной матрицы и решите систему:
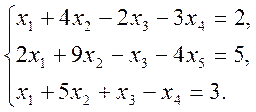 .
.
Вычислим ранг матрицы из коэффициентов системы:
A = 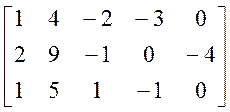 ®
® 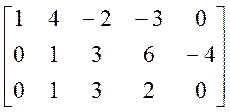 ®
® 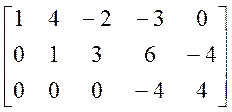
Þ RA = 3.
Теперь находим ранг расширенной матрицы:
A* =  ®
® 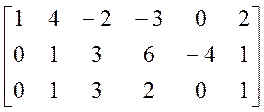 ®
® 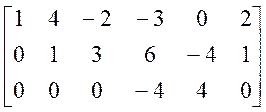 (*)
(*)
Þ RA* = 3
Число неизвестных m = 5.
Так как RA = RA* = R = 3 система совместна. Но при этом R меньше числа неизвестных и и при этом число свободных переменных m – R = 5 – 3 = 2. Следовательно
Напишем систему, равносильную исходной, расширенной матрицей которой является матрица (*):
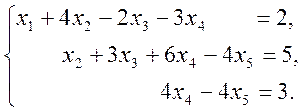 0матриНаходим
решение системы
0матриНаходим
решение системы
Пусть x5 = a. Но тогда x4 =x5 = a ( из последнего уравнения -4x4 + 4x5 = 0).
Положим теперь x3 = b и тогда:
x2 + 3x3 + 6x4 – 4x5 = 1
x2 + 3x3 + 2a = 1
x3 = b
x2 = 1 - 2a - 3b
x1 + 4x2 – 2x3 – 3x4 = 2
x1 = 2 – 4x2 + 2x3 + 3x4
x1 = 2 – 4 × (1 - 2a - 3b) + 2b + 3a
x1 = 2 – 4 +8a + 12b + 2b + 3a = 11a + 14b -2
Ответ:
X = 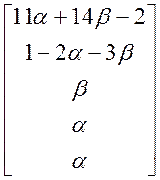
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.