Образец выполнения домашнего задания по теме "Линейная алгебра"

                 Образец выполнения домашнего задания по теме

                                              ЛИНЕЙНАЯ АЛГЕБРА  2

1)  Образует ли линейное пространство множество всех дифференцируемых функций, в котором определены сумма любых двух элементов a и b и произведение любого элемента α (сумма: f(t)·g(t), произведение α·f(t))?

Да,  образует:

1.  «Сумма»  (в  рассматриваемом случае произведении  )  двух  дифференцируемых  функций  f(t)  иg(t),  равная   f(t)·g(t) -  есть  функция  дифференцируемая.

2.   f(t) ×g(t)= g(t) ×f(t)×

3.  f(t) × (g(t) ×(t))=(f(t) ×g(t)) ×(t)

4. (t),  f(t) ××1=1×f(t)=f(t).   Т.е.  функция  (t) - это  нейтральный  элемент  при  «сложении»  функций.

5.  Операция  умножение  af(t),  a   заведомо  удовлетворяет  аксиомам умножения  вектора  на  число:

                                 1. (af(t)) ×g(t)= a(f(t) ×g(t))

2. (ab)f(t)=a(bf(t))

                                  3. 1·f(t)=f(t)

4. (a+b)f(t)=af(t)+bf(t)

2)  При каких α система векторов линейно-зависима?:

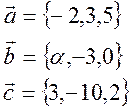
Решение:

      Если  система  векторов  ,  линейно-зависимая,  то  должны  найтись  такие  

      числа    не  все  равные  нулю,  чтобы  выполнялось  равенство

        (1).  Это  векторное  уравнение  равносильно  системе  

      уравнений:

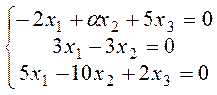                                                                       (2)

      Система  (2) – однородная  линейная  система,  имеющая в случае линейной зависимости системы  векторов  ,  ненулевые  решения, только в том случае ,      если  определитель  этой  системы  равен  нулю  (ранг  матрицы  системы  меньше  3)

      .  Следовательно,  должно  быть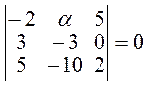          

            ,  .

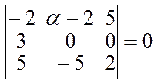
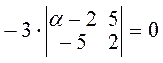
      Ответ:

3)  Найти координаты вектора , заданного в базисе , в новом базисе , если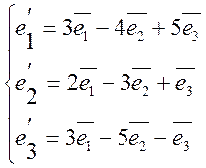

Решение:

          Пусть  - координаты вектора  в новом базисе.

a)  способ     - суть  решения  системы     .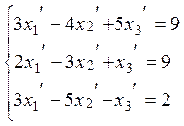

Решаем  систему  методом  Гаусса:

            

 

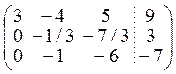
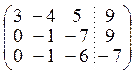
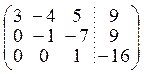
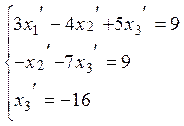
2     способ    Найдем 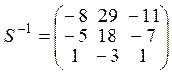 .  Тогда: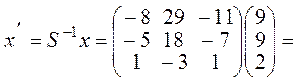 

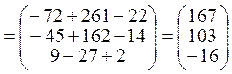.  Координаты  вектора    в  новом  базисе.

Ответ:

4)  Найдите матрицу линейного оператора в базисе , где   если в базисе  она имеет вид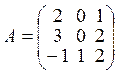

Решение:

  Пусть  - матрица перехода от старого базиса к новому. Тогода:

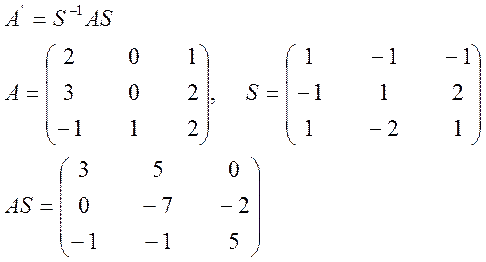             и

            Найдем  :

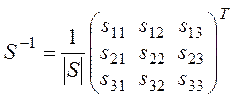            ,   - алгебраические  дополнения  элементов определителя матрицы ,    а     -  определитель  матрицы  S. Найдем определитель  матрицы  S:

            .

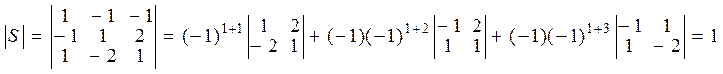
            Теперь последовательно находим :

           

           

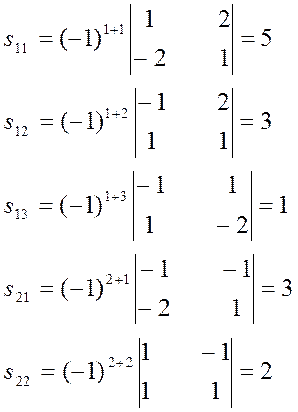
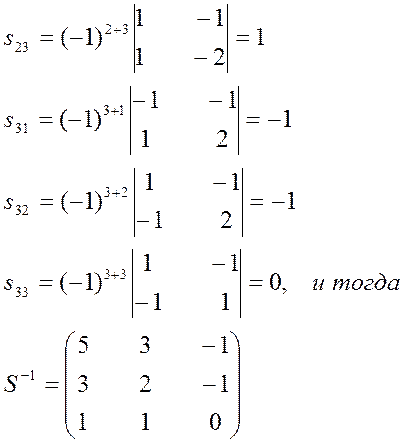
            И , следовательно, 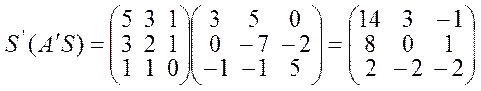  - матрица  линейного     преобразования  в  новом  базисе.