Домашнее индивидуальное задание. № 4 (Тереханов В.В.)
Матрица преобразования
заключающегося в масштабировании с координатами 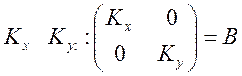
Итоговая матрица преобразования С=A*B
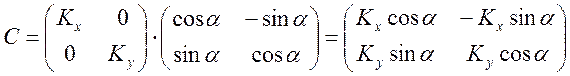
Ответ: 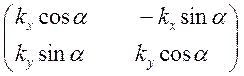
Симметрия относительно плоскости ХОУ означает что для любой точки А с координатами x,y,z сопоставляется точка с координатами x,y,-z
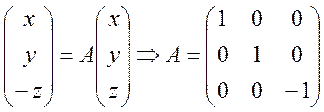
Ответ: 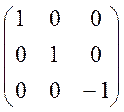
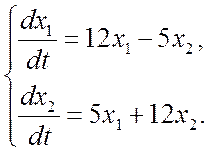
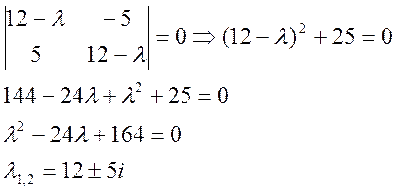
![]()
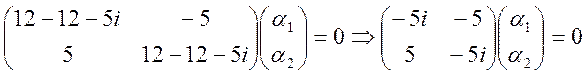
![]()
![]() собственный вектор
собственный вектор 
![]()
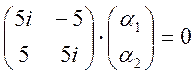
![]() второй
вектор
второй
вектор ![]()
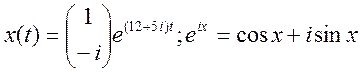
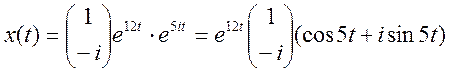
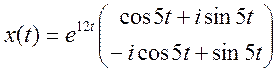
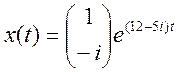
Ответ: 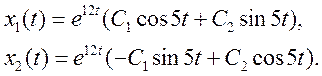
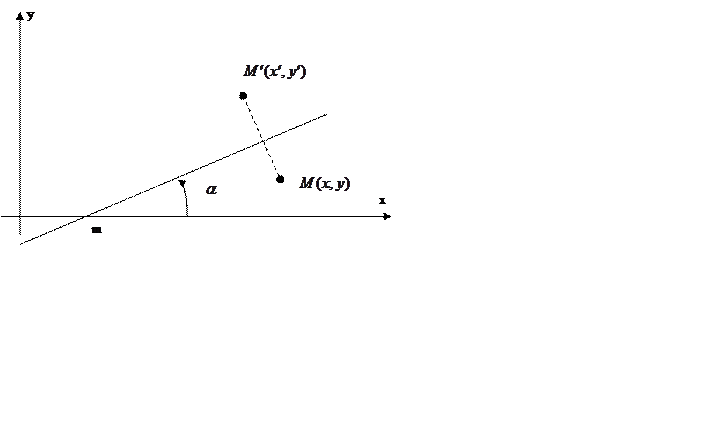
Указание. Рассмотреть
последовательность трех преобразований – параллельного сдвига оси симметрии на
вектор ![]() , выполнение симметричного
преобразования относительно оси, проходящей через начало координат, возвращение
оси в исходное положение.
, выполнение симметричного
преобразования относительно оси, проходящей через начало координат, возвращение
оси в исходное положение.
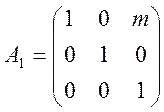
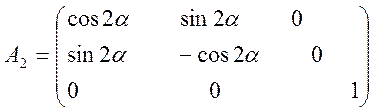
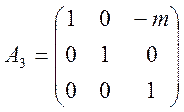
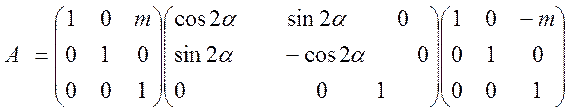 =
=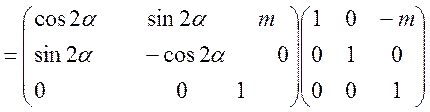
Ответ: 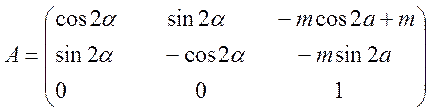
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.