Задачей кинематического анализа механизма является определение положений звеньев в пределах одного периода движения; построения траекторий для характерныхих точек; определение линейных скоростей и ускорений этих точек, а также угловых скоростей и ускорений звеньев.
В задачи кинематического исследования механизмов входят:
1. Определение положений звеньев, включая определение траекторий отдельных точек звеньев (решается построением планов положения звеньев)
2. Определением скоростей и ускорений (линейных и угловых) звеньев и отдельных точек.
При решении этих задач (1 и 2) должны быть известны : законы движения ведущего звена (кривошипа) и кинематическая схема механизма с указанием размеров звеньев. Как правило, кривошипы совершают равномерное вращательное движение (вращение ω=const, ε=0).
Построение плана положений.
Вычисляем масштаб построения планов положений звеньев механизма. План строится методом засечек , для вычисления масштаба μl необходимо задать чертежное изображение длины кривошипа.
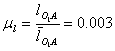
![]()
Затем с помощью масштабного коэффициента переводим истинные длины звеньев механизма в чертежные.

При построении планов положений необходимо найти крайние положения звеньев, т.е. положения при которых кривошип и шатун располагаются вдоль одной оси.
Начиная от найденного крайнего положения траекторию движения (А0) кривошипа необходимо поделить на 8 равных частей по направлению движения и зафиксировать 8 положений кривошипа и обозначить А1 А2 А3 А4 и т.д. Далее пользуясь методом засечек найти все остальные.
Центр тяжести второго звена S2 располагается посередине АВ, центр тяжести третьего звена S3 находится на пересечении медиан треугольника О3ВС.
Построение планов скоростей механизма.
Линейные скорости всех характерных точек механизмов определяются методом построения планов скоростей. Для этого предварительно составляются векторные уравнения выражающие собой полную скорость соответствующей точки звена из условия рассмотрения движения этой точки отдельно с каждым из звеньев. Графическое решение этих уравнений позволяет получить соответствующие планы скоростей.
Построение планов скоростей механизма.
Вычисляем угловую и линейную скорости входного звена:
![]()
![]()
Зададимся чертежным изображением вектора скорости точки А и вычислим масштабный коэффициент плана скоростей.
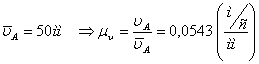
Вектор скорости точки А перпендикулярен звену ОА и направлен в сторону вращения этого звена.
Для построения плана скоростей звеньев механизма, необходимо составить векторное уравнение, графическое изображение которых позволяют найти скорости и векторы. Точка В принадлежит к двум звеньям 2 и 3. Для составления интересующих векторных уравнений необходимо рассмотреть движение точки В отдельно с каждым звеном.
Построение плана скоростей на примере 8-го положения.
Рассмотрим движение точки В относительно точки А и стойки.
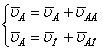
Звено 3 совершает вращательное движение, значит скорость точки В относительно стойки перпендикулярна О3В . Проведем линию действия скорости точки В относительно стойки через полюс плана скоростей. Затем через точку А на плане скоростей проведем линию действия скорости точки В относительно точки А (перпендикулярно чертежному изображению АВ). Точка пересечения этих двух линий будет являться решением системы уравнений, то есть точкой В. Из полюса проведем скорость точки В. Скорость точки С строится аналогично скорости точки В. Треугольник О3ВС на плане ускорений подобен треугольнику О3ВС на плане положений. S2 лежит посередине АВ. S3 лежит на пересечении медиан треугольника О3ВС, проведем скорость центра масс третьего звена из полюса. Получив чертежные изображения скоростей всех характерных точек механизма, найдем их истинное значение с помощью масштабного коэффициента плана скоростей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.