Исследование прохождения сигнала через четырехполюсник, страница 3

Определение переходных характеристик путем решения дифферинциальных уравнений

Определим характеристическое уравнение из условия свободного режима в цепи (U = 0).

Для этого применим к дифференциальным уравнениям переменных состояния прямое  преобразование Лапласа:

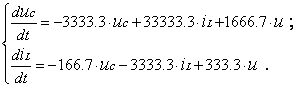
Для определения характеристического уравнения нужно исключить внешнее воздействие (U(p) = 0), составить определитель системы этих уравнений и приравнять его нулю:

Характеристическое уравнение:  .

Корни характеристического уравнения:   ; 

                                                                    .

Корни характеристического уравнения - комплексно сопряженные, поэтому свободные составляющие напряжения на конденсаторе  и тока в индуктивности  ищутся в виде:

Определение переходных характеристик по схемам замещения

Определяем постоянные интегрирования A, B, ,   из начальных и конечных условий.

Конечные условия определяются из схемы замещения цепи при t =  и определяют

вынужденные составляющие при единичном входном воздействии (U = 1 B):

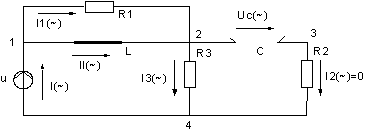
Рис.3 Схема замещения для установившегося режима (t = ).