Побудова прогнозу, використовуючи метод ковзної середньої

2.2. Побудова прогнозу використовуючи метод ковзної середньої

Таблиця 2.1 – Розроблення прогнозу за допомогою методу ковзної середньої

№ Періоду	Фактичні значення змінної	Прогнозні значення змінної
1.	136,3
2.	124,4
3.	137,7
4.	133,4	132,8
5.	137,0	131,83
6.	130,0	136,03
7.	135,3	133,47
8.	136,4	134,1
9.	134,4	133,9
10.	139,3	135,37
11.	134,5	136,7
12.	141,0	136,06
13.		138,27

Розрахунок ковзної середньої здійснюється за формулою :

X_сер.=;                                                                                               (2.1)  де  X_сер. – середнє значення змінної; X_1,X_2,X₃ – фактичні значення змінної .

X₄=  132,8

X₅=  131,83

X₆=  136,03

X₇=  133,47

X₈=  134,1

X₉=  133,9

X₁₀=  135,37

X₁₁=  136,7

X₁₂=  136,06

X₁₃=  138,27

Побудуємо графік, який відображає криві фактичних та прогнозних значень у відповідні проміжки часу.

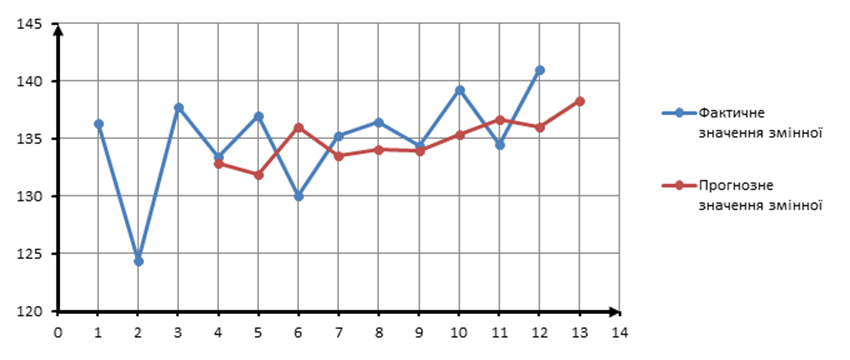
Рис 2.1. - Графічне відображення фактичних та прогнозних значень змінної при використанні методу ковзної середньої.

Визначимо похибку (середнє квадратичне відхилення) для визначення помилки в прогнозуванні.

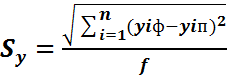 ;                                                                             (2.2)            де S_y – середнє квадратичне відхилення; yiф – фактичне значення змінної; yiп – прогнозне значення змінної; f – кількість ступенів свободи ряду.

f = n - m(2.3)

де n – кількість спостережень; m – кількість параметрів, що оцінюються.

f = 9 - 2= 7

S_y=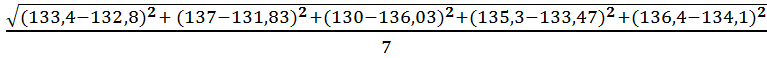

=

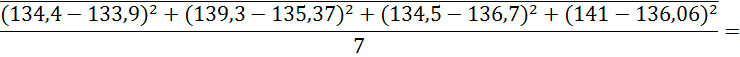
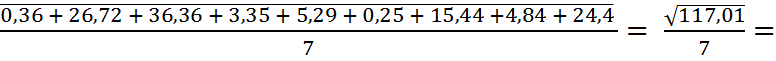
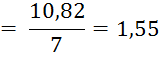
Визначаємо довірчий інтервал :

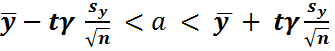                                                                          (2.4)

де   - прогнозне значення ряду; - залежність надійності від кількості спостережень;  - середнє квадратичне відхилення; n – кількість спостережень; а – параметр прогнозування.

Знайдемо залежність надійності за таблицею:

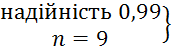   = tγ = 2,36

138,27 – 2,36  а  138,27 + 2,36 ;

137,05 а139,49

2.3 Розробка прогнозу при використанні методу найменших квадратів

Таблиця 2.2 – Вихідні дані для прогнозування за методом найменших квадратів

№ Періоду	Фактичні значення змінної	Прогнозні значення змінної
1.	136,3	131,84
2.	124,4	132,41
3.	137,7	132,98
4.	133,4	133,55
5.	137,0	134,12
6.	130,0	134,69
7.	135,3	135,26
8.	136,4	135,83
9.	134,4	136,4
10.	139,3	136,97
11.	134,5	137,54
12.	141,0	138,11
13.		138,68

Для розробки прогнозу за методом найменших квадратів необхідно розв’язати систему рівнянь та визначити лінійний взаємозв’язок між результатами спостережень і часом за якій ці спостереження здійсняться.

(2.5)

де y – прогнозне значення змінної; х – період спостереження; а_0,а₁ – параметри прогнозування.

;

 ;

  ;     ;

 

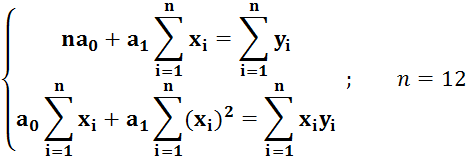
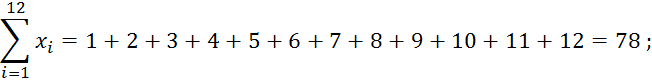
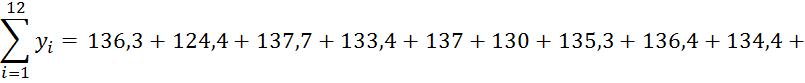
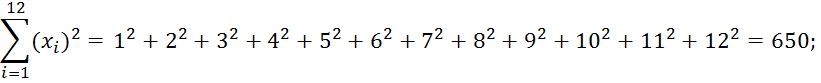
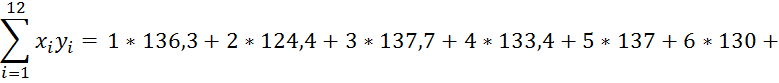
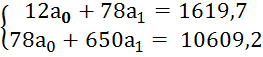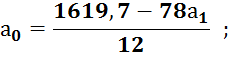
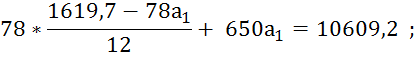
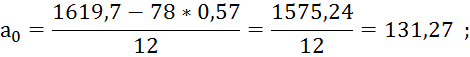
Перевіримо правильність розв'язання підставивши значення  до одного з рівнянь системи:

Отримані значення параметрів підставляємо в формулу (2.5) :

Побудуємо графік, який відображає криві фактичних та прогнозних значень у відповідні проміжки часу :

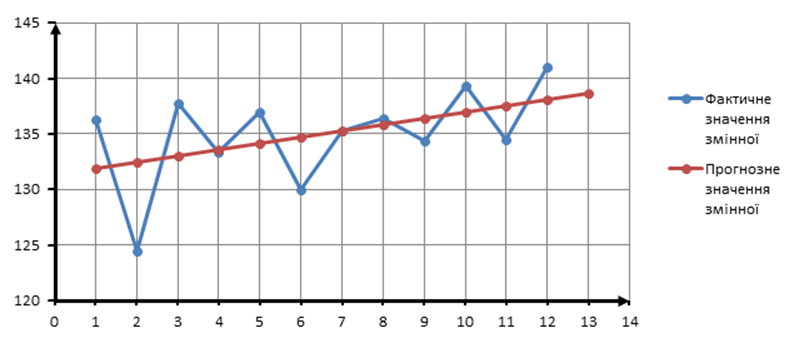
Рис 2.2 - Графічне відображення фактичних та прогнозних значень при використанні методу найменших квадратів

Визначимо похибку прогнозування за формулою (2.2) :

 

 

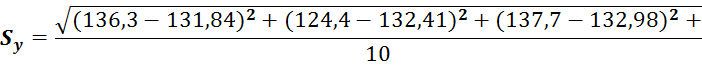
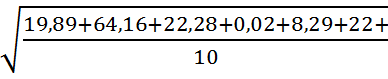
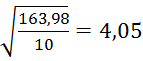
Визначаємо довірчий інтервал за формулою (2.4) :

Знайдемо залежність надійності за таблицею:

 ;

;

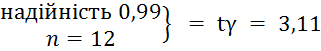Висновок :

З двох розроблених прогнозів можна зробити висновок, що прогноз побудований за допомогою методу ковзної середньої є більш точним ніж прогноз, побудований за допомогою методу найменших квадратів, оскільки середнє квадратичне відхилення методу найменших квадратів більше ніж методу ковзної середньої . Але на графіку пряма методу найменших квадратів недостатньо чітко відображає динаміку зміни явищ.