Побудова прогнозу, використовуючи метод ковзної середньої, страница 2

3. Розробка моделі для розв'язання оптимізаційної задачі

Таблиця 3.1 - Вихідні дані для оптимізаційної задачі

Сировина	Норми розходу компоненту на 1 кг продукції , кг		Виробнича потужність підприємства, кг
	Ковбаса	Фарш
Яловичина	0,75	0,8	15000
Свинина	0,15	0,19	5000
Харчові добавки	0,1	0,01	400
Ціна реалізації одиниці продукції	30	20

Знаходимо систему обмежень. Нехай:

x₁ – ковбаса;  x₂ – фарш, тоді:

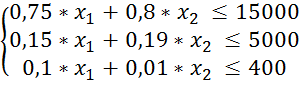                                                                                     (3.1)

де  x₁ ≥ 0;  x₂ ≥ 0

Для знаходження максимального прибутку використовується цільова функція типу:

L = 30 X₁ * 20 X₂ → max                                                                                               (3.2)

Розглянемо третє рівняння системи. Нехай x₁ = 0, тоді  0,01x₂ = 400;  x₂ = 40000 (кг)

Нехай x₂ = 0, тоді  0,1x₁ = 400,       x₁=4000 (кг)

Скоригуємо отримані результати на величину випадкових чисел. Знайдемо X₁ та X₂ використовуючи послідовно пари випадкових чисел. Перевіримо систему обмежень, в разі відповідності  обмеженням знайдемо значення цільової функції.

R₁ = 2;  R₂ = 55.

X₁ = x_{1 *}   X₂ = x_{2 *}

Знайдемо X₁ та X₂ :

X₁ = 4000  (кг);   X₂ = 40000  (кг)

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

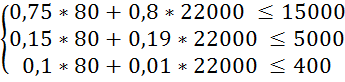
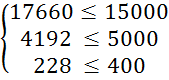       Ø; L₁ – знайти неможливо.

Використаємо другу пару випадкових чисел R₁ = 28; R₂ = 27;

Знайдемо X₁ та X₂ :

X₁ = 4000  1120 (кг);   X₂ = 40000  10800 (кг)

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

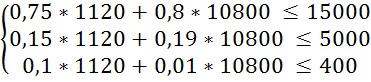
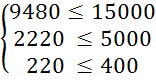
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₂ = 30 * X₁ + 20 * X₂ = 30 * 1120 + 20 * 10800 = 249600 (грн.)

Використаємо третю  пару випадкових чисел R₁ = 49; R₂ = 15;

Знайдемо X₁ та X₂ :

X₁ = 4000  1960 (кг);  X₂ = 40000  = 6000 (кг)

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

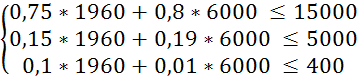
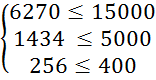
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₃ = 30 * X₁ + 20 * X₂ = 30 * 1960 + 20 * 6000 = 58800 + 120000 = 178800 (грн.)

Використаємо четверту  пару випадкових чисел R₁ = 36;  R₂ = 18.

Знайдемо X₁ та X₂ :

X₁ = 4000  1440 (кг);   X₂ = 40000  = 7200 (кг).

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

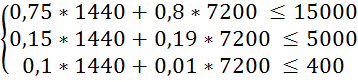
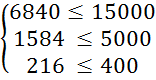
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₄ = 30 * X₁ + 20 * X₂ = 30 * 1440 + 20 * 7200 = 187200 (грн.)

Використаємо п’яту   пару випадкових чисел R₁ = 22;  R₂ = 50.

Знайдемо X₁ та X₂ :

X₁ = 4000 880 (кг);   X₂ = 40000  = 20000 (кг)

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

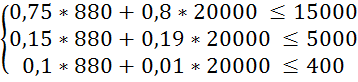
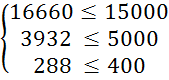          Ø; L₅ – знайти неможливо.

Використаємо шосту  пару випадкових чисел R₁ = 10;  R₂ = 12.

Знайдемо X₁ та X₂ :

X₁ = 4000  400 (кг);    X₂ = 40000  = 4800 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

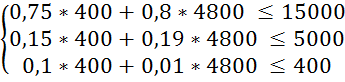
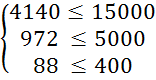
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₆ = 30 * X₁ + 20 * X₂ = 30 * 400 + 20 * 4800 = 108000 (грн.)

Використаємо сьому  пару випадкових чисел R₁ = 88;  R₂ = 4.

Знайдемо X₁ та X₂ :

X₁ = 4000  3520 (кг);   X₂ = 40000  = 1600 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

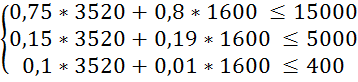
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₇ = 30 * X₁ + 20 * X₂ = 30 * 3520 + 20 * 1600 = 137600 (грн.)

Використаємо восьму  пару випадкових чисел R₁ = 41;  R₂ = 67.

Знайдемо X₁ та X₂ :

X₁ = 4000  1640 (кг);   X₂ = 40000  = 26800 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

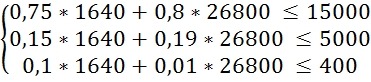
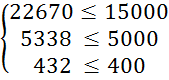         Ø; L₈ – знайти неможливо.

Використаємо дев'яту пару випадкових чисел R₁ =72;  R₂ = 18.

Знайдемо X₁ та X₂ :

X₁ = 4000  2880 (кг);   X₂ = 40000  = 7200 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

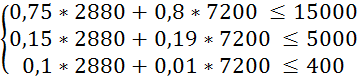
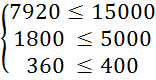
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₉ = 30 * X₁ + 20 * X₂ = 30 * 2880 + 20 * 7200 = 230400 (грн.) 

Використаємо десяту  пару випадкових чисел R₁ = 33;  R₂ = 11.

Знайдемо X₁ та X₂ :

X₁ = 4000  1320 (кг);   X₂ = 40000  = 4400 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

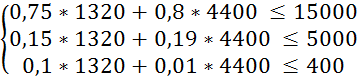
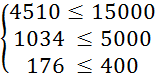
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₁₀ = 30 * X₁ + 20 * X₂ = 30 * 1320 + 20 * 4400 = 127600 (грн.)

Використаємо одинадцяту пару випадкових чисел R₁ = 53;  R₂ = 66.