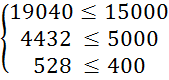Побудова прогнозу, використовуючи метод ковзної середньої, страница 4

   Ø; L₂₆ – знайти неможливо.

Використаємо двадцять сьому пару випадкових чисел R₁ = 37;  R₂ = 77.

Знайдемо X₁ та X₂ :

X₁ = 4000  1480 (кг);  X₂ = 40000  = 30800 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

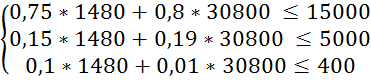
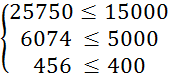 Ø; L₂₇ – знайти неможливо.

Використаємо двадцять восьму пару випадкових чисел R₁ = 7;  R₂ = 79.

Знайдемо X₁ та X₂ :

X₁ = 4000  280 (кг);  X₂ = 40000  = 31600 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

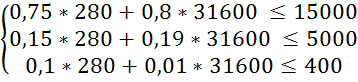
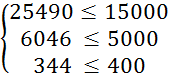 Ø; L₂₈ – знайти неможливо.

Використаємо двадцять дев'яту пару випадкових чисел R₁ = 8;  R₂ = 13.

Знайдемо X₁ та X₂ :

X₁ = 4000  320 (кг);  X₂ = 40000  = 5200 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

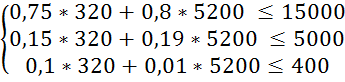
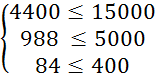
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₂₉ = 30 * X₁ + 20 * X₂ = 30 * 320 + 20 * 5200 = 113600 (грн.)

Використаємо тридцяту пару випадкових чисел R₁ = 9;  R₂ = 10.

Знайдемо X₁ та X₂ :

X₁ = 4000  360 (кг);  X₂ = 40000  = 4000 (кг);

Перевіримо систему обмежень підставивши отримані результати в систему (3.1):

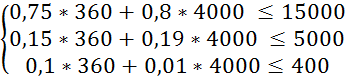
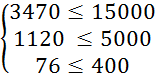
Оскільки обмеження виконується знайдемо значення цільової функції  за формулою (3.2):

L₃₀ = 30 * X₁ + 20 * X₂ = 30 * 360 + 20 * 4000 = 90800 (грн.)

Заносимо отримані результати до таблиці.

Таблиця 3.2 - Результати розрахунків

Продовження таблиці 3.2 – Результати розрахунків

Продовження таблиці 3.2 – Результати розрахунків

Отже за критерієм максимізації прибутку оптимальним є п’ятнадцятий варіант, тобто при виробництві та реалізації 760 (кг) ковбаси за ціною 30 (грн./кг), та 17600 (кг) фаршу за ціною (20 грн./кг), не формуючи залишків, підприємство отримає максимальний прибуток в розмірі 374800 (грн.)    Із всіх випробувань 50 % виявились не результативними.