Векторная алгебра. Векторно-скалярное произведение. Двойное векторное произведение

Занятие 2.

Векторная алгебра.

Вектором называется величина, характеризующая помимо измеряющего в определённых единицах числа, ещё своим направлением в пространстве.

Численное значение вектора называется величиной, модулем или длиной вектора.

Для численного задания вектора нужно указать три числа. Это либо длина вектора и направление, которое задается двумя числами, либо три скалярных величины.

Поэтому равенство трёх векторов сводится к равенству попарно трёх чисел, эти векторы определяющих.

Вывод: Одно векторное равенство равно трём скалярным равенствам.

Различают векторы трёх видов: свободные передвижные и определенные векторы.

Точку приложения свободных векторов можно выбирать произвольно.

У передвижных векторов точку приложения вектора можно перемещать вдоль самого вектора.

У определённых векторов точка приложения вектора должна быть зафиксирована.

Изучение передвижных и определённых векторов сводится к изучению свободных векторов, поэтому достаточно ограничиться рассмотрением только свободных векторов.

1. Сумма векторов. Чтобы получить вектор , представляющий геометрическую сумму двух векторов  и , надо от произвольной точки А пространства отложить вектор , к концу его приложить начало вектора , тогда  по величине и направлению представляет вектор .

Рис. 1. Сложение векторов.

2. При сложении нескольких векторов каждый последующий вектор складывается с суммой предыдущих векторов.

Для вычитания вектора  из вектора  необходимо прибавить к вектору  вектор -, противоположный вектору .

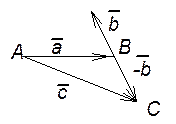
Рис. 2. Вычитание векторов.

3. Умножение вектора на целое положительное число. Умножить вектор  на целое положительное число m – значит сложить между собой m векторов равных .

4. Два параллельные между собой вектора называются коллинеарными.

5. Если векторы  и  не коллинеарны, то вектор  параллелен плоскости, определяемый векторами  и .

В этом случае говорят, что векторы , , , компланарны, т.е. параллельны одной плоскости.

6. Если три вектора ,  и  не компланарны, то всяких вектор  может быть представлен в форме , т.е. разложен на три составляющие параллельные соответственно векторам ,  и .

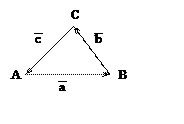Задача 1.      Какому условию должны удовлетворять три вектора ,  и , чтобы из них можно было образовать треугольник.

Из чертежа видно, что сумма векторов ,  и  должна быть равна нулю.              .

Задача 2.      Найти радиус-вектор  середины С отрезка АВ, зная точки ,

Понятие радиус-вектора.

Положение какой-либо точки пространства может быть определено вектором, соединяющим рассматриваемую точку с начальной произвольно выбранной точкой (началом координат).

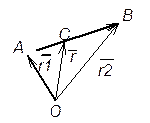Будем называть вектор , имеющий начало в точке О, а конец в точке Р радиус-вектором точки Р относительно точки О и будем его обозначать как . Про точку Р будем говорить, что дана точка .

Имеем вектор, соединяющий точки  и 

                         .

Задача 3.      Доказать, что если диагонали четырехугольника делят друг друга пополам, то четырех угольник есть параллелограмм.

Решение              ;      ;     Отсюда                   или  , т.е. .

Это означает, что сторона АВ = DC и АВ || DC. Т.е. четырехугольник - параллелограмм.

Скалярное или внутреннее произведение двух векторов.

Скалярным или внутренним произведением двух векторов  и  называется произведение длин обоих векторов, умноженное на косинус угла между обоими векторами.               

В результате получаем скаляр.

Скалярное произведение равно произведению длины одного из векторов на проекцию другого вектора на направление первого.

Важнейшие свойства скалярного произведения.

1.           

2.           

3.            , если  или  или

4.            , если a и b коллинеарны, в частности

5.           

6.           

7.           

Задача 4.      Дан треугольник ΔАВС.

Вывести основную формулу геометрии 

Из рисунка имеем           

Умножим скалярно                

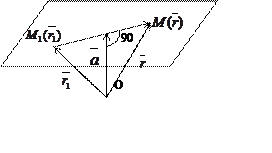
Задача 5.      Найти уравнение плоскости, перпендикулярной к заданному вектору  и проходящий через точку .

Возьмем любую точку  плоскости, тогда вектор  лежит в плоскости, а вектор  перпендикулярен плоскости. Уравнение  представляет уравнение некоторой плоскости О.

Векторное или внешнее произведение двух векторов.

Векторным или внешним произведением двух векторов  и  называется вектор