Основы финансовой математики: Учебно-методическое пособие

Альтернативное решение можно проиллюстрировать временной диаграммой:

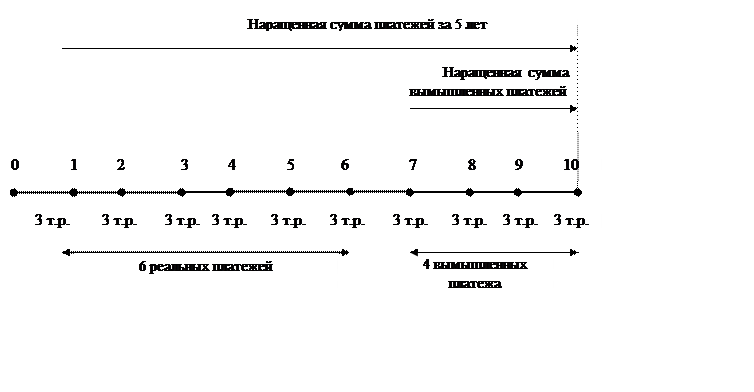
Рис. 14. Временная диаграмма примера 23

В расчетах коэффициенты наращения аннуитета взяты из табл. 3 прил. 2.

Для определения современного (или текущего) значения аннуитета необходимо просуммировать текущие величины каждого платежа.

Пример 24.

Найти современную величину аннуитета для четырех платежей по 5 тыс. руб., которые вносились на счет в конце каждого года под 12 %.

Решение.

Для текущего аннуитета точкой локализации является начало аннуитета. Все платежи надо привести к этой точке, полученные значения сложить.

По формуле (15) найдем современное значение каждого платежа:

для первого платежа Р₁ = 5  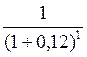= 4,465 тыс. руб.;

для второго платежа Р₂ = 5  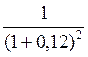= 3,985 тыс. руб.;

для третьего платежа Р₃ = 5  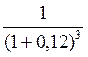= 3,56 тыс. руб.;

для четвертого платежа Р₄ = 5  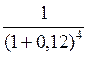= 3,18 тыс. руб.;

Сумма всех дисконтированных платежей составит:

4,465 + 3,985 + 3,56 + 3,18 = 15,19 тыс. руб.

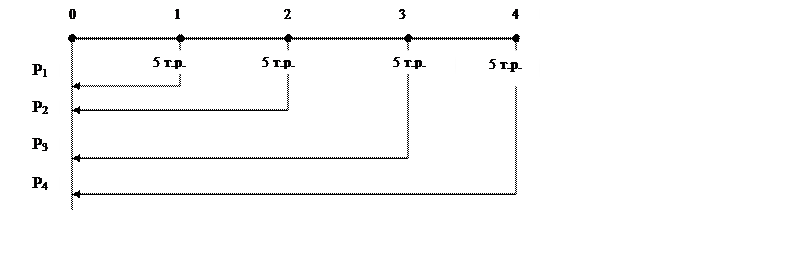
Рис. 15. Временная диаграмма примера 24

Если число платежей невелико, расчет можно вести так, как было сделано в примере. Но в любом случае проще воспользоваться формулой:

А_об. = R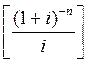= R k                          (23)

где А_об. – современная величина обыкновенного аннуитета;

i – годовая процентная ставка;

n – число платежей;

R – периодический платеж.

Выражение в квадратных скобках является коэффициентом дисконтирования аннуитета (k). Его можно определить по табл. 4 прил. 2.

Воспользуемся формулой (23) и табл. 4 прил. 2 для решения выше приведенного примера:

А_об. = 5  3,037 = 15,19 тыс. руб.

Результат получим такой же, но решение намного проще.

Зная современное значение аннуитета, можно определить величину периодического платежа:

R = A                                               (24)

Пример 25.

Заемщик берет ссуду в 100 млн руб. под 10 % и должен погасить ее равными платежами в конце первого, второго и третьего года. Какими должны быть ежегодные платежи?

Решение.

Поскольку имеют место платежи, речь идет об аннуитетах. Известна современная величина аннуитета, т.к. ссуду заемщик берет сейчас, в настоящее время.

Для решения воспользуемся формулой (24) и табл. 4 прил. 2:

R = 100 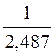= 40, 21 млн руб.

Пример 26.

Заемщик берет ссуду на 3 года из расчета 10 % годовых. Она должна быть погашена тремя платежами по 1 млн руб. в конце первого, второго и третьего года. Какую сумму рассчитывает получить заемщик?

Решение.

А_об.  = 1  2,487 = 2,487 тыс. руб.

Пользуясь таблицами, рассчитать параметры аннуитета несложно, но надо быть внимательным, чтобы не перепутать современную и будущую величину аннуитета.

Как было сказано выше, аннуитет может быть не только обыкновенным, но и срочным.

Срочный аннуитет  отличается осуществлением платежей не в конце, а в начале каждого интервала начисления. Это значит, что первый платеж проводится сразу же, а не через год. В отличие от обыкновенного аннуитета, на последний платеж срочного аннуитета проценты начисляются.

Примерами срочного аннуитета являются страховые взносы, арендная плата.

Чтобы вывести формулу будущей величины срочного аннуитета, модифицируют формулу (21).Это позволяет пользоваться таблицами коэффициентов обычного аннуитета.

Сравним срочный и обыкновенный аннуитеты с помощью временной диаграммы. Заметим, что срочный аннуитет начинается сразу же с первого платежа, а заканчивается одним периодом после последнего n-го платежа.

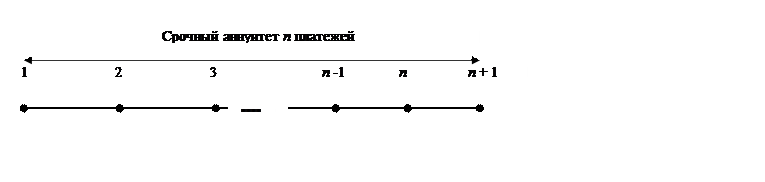
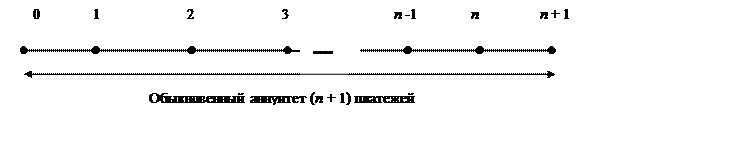
Рис. 16. Временная диаграмма обыкновенного и срочного аннуитетов

Рис. 16 показывает, что на основе расчета будущей величины обыкновенного аннуитета, состоящего из (n + 1) платежей, можно определить будущее значение срочного аннуитета, но состоящего из n платежей, поскольку последний (n + 1) платеж реально не сделан к концу последнего периода срочного аннуитета.

Таким образом, чтобы найти будущую величину срочного аннуитета, надо вычесть один платеж из будущего значения обыкновенного аннуитета, число платежей которого на 1 больше, чем у срочного аннуитета.

S,                                                  (25)

где S- будущая величина срочного аннуитета, состоящего из n платежей;

S - будущая величина обыкновенного аннуитета, состоящего из ( n+1) платежей.

После преобразований формула (25) имеет следующий вид:

S= R (k - 1),                                          (26)

где k - коэффициент наращения обыкновенного аннуитета, состоящего из (n+ 1) платежей.

Формула (26) позволяет пользоваться табличными значениями коэффициентов наращения обыкновенных аннуитетов.

Пример 27.

Платежи в размере 10 тыс. руб. перечисляются на накопительный счет в начале каждого года. На них начисляются проценты по ставке 8 %. Какая сумма будет на счете к концу 5^го года?

Решение.

Поскольку речь идет о срочном аннуитете, то для нахождения