Определение манометрического давления в верхней части одного из сообщающихся сосудов, наполненных водой, под действием силы, приложенной к поршню правого сосуда

Министерство образования Российской Федерации

Карельский региональный институт управления, экономики и права

Петрозаводского Государственного Университета при правительстве РК

Кафедра: Энергообеспечение предприятий

Курс “Гидравлика”

Курсовой проект

«Решение задач»

Выполнил: студент 1 курса группы ЭП-7

Краснопёров Сергей Владимирович

Научный руководитель:

Беляев Сергей Васильевич

Петрозаводск 2003 г.

Содержание

1.  Гидростатика

1.1.  Задача 3 в-9         стр.3

1.2.  Задача 4 в-9         стр.4    

2.  Гидродинамика

2.1.  Задача 16 в-9       стр.6

2.2.  Задача 21 в-9       стр.7      

2.3.  Задача 23 в-9       стр.9

2.4.  Задача Д6 в-17   стр.11

3.  Список используемой литературы  стр.14

1.Раздел: Гидростатика

1.1.  Задача3 в-9

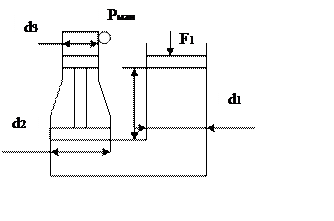
Определить манометрическое давление Рман  в верхней части одного из сообщающихся сосудов, наполненных водой, под действием силы F1 , приложенной к поршню правого сосуда.

Исходные данные:

Решение:

Для определения манометрического давления рассмотрим условие равновесия поршня в левом сосуде:

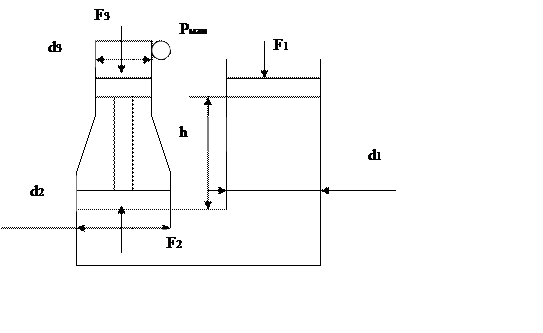Поршень находится под действием сил F2 и F3. Для нахождения поршня в равновесии необходимо выполнение условия: F2 = F3.

Где  F3=Pм ·πd3²/4 . Силу F2 можно найти, определив давление воды на поршень снизу. Для определения этого давления проведем поверхность уровня равного давления и определим на ней точки: (а) и (а1).

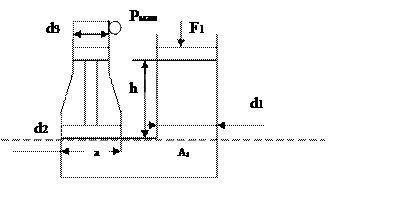Давление в точке (а) будет равно давлению в точке (а1), т.е. Ра = Ра₁. Давление в точке (а1) определяется по формуле  Ра₁=Р1+ρgh, где Р1 – давление внешнее определяется по формуле Р1=F1/πd1²/4, а ρgh  - избыточное давление. Здесь ρ – плотность (для воды ρ = 1000 кг/ м³), g – ускорение свободного падения = 9,8м/с², h – высота столба жидкости. Отсюда мы можем определить силу,  действующую на поршень снизу F2 = Pa ·  πd2²/4.

Подставим определённые величины в уравнение равновесия, получим:     

Paπd2²/4= Pм ·πd3²/4, помножим правую и левую части уравнения на 4/π, отсюда манометрическое давление Рм = Ра · d2²/d3².

Подставляем исходные данные в имеющиеся формулы: Р1 = 350/3,14 · 20²/4 =1,115 кг/см², для дальнейших расчётов давление необходимо перевести в [Па]:

Р1 = 1,115 · 98000 = 109270Па

Ра = 109270 + 1000 · 9,8 · 1,1 = 120050Па

Следовательно: Рм = 120050 · 0,3²/0,15² = 480200Па или ≈ 4,9 кг/см²

Ответ: манометрическое давление в верхней части одного из сообщающихся сосудов будет приблизительно равно 4,9 кг/см², что больше в несколько раз давления действующего извне. Такое устройство называется мультипликатором и служит для повышения давления.

1.2  Задача 4 в-9

Определить высоту h, на которую может поднять воду прямодействующий паровой насос при следующих данных: d1 = 200мм; d2 = 450мм; Рман = 3кг/см²

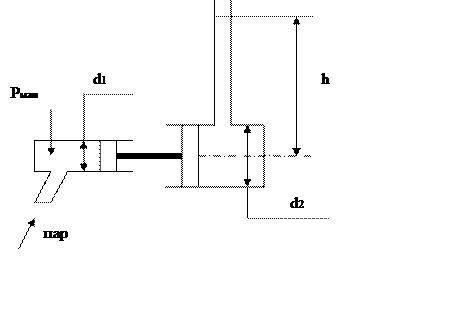Решение:

При достижении жидкостью максимальной высоты установится равновесие, т.е. сила, действующая с левой стороны на поршень (F1) будет по величине равна силе действующей на поршень с правой стороны (F2). Силу, действующую с левой стороны можно определить по формуле: F1 = Pман · π d1²/4. Так как Pман является давлением избыточным, то для данного случая оно будет преодолевать избыточное давление со стороны жидкости и силу, действующую с правой стороны можно определить по формуле:

F2 = Ризб · πd2²/4, где Ризб – избыточное давление, действующее на поршень со стороны жидкости.

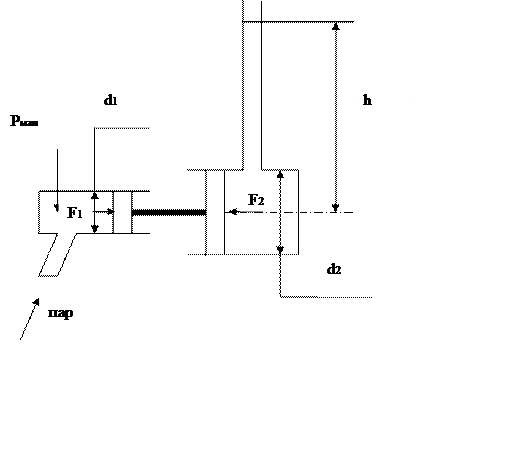Избыточное давление, действующее со стороны жидкости, можно определить по формуле: Ризб  = ρgh, где ρ- плотность (для воды ρ = 1000 кг/м³), h – высота столба жидкости в [м], а g – ускорение свободного падения = 9,8м/с². Избыточное давление на разной глубине имеет разное значение, но для данного случая, взяв среднюю величину избыточного давления, мы получим туже формулу.  

При подставлении в уравнение равновесия найденных значений (F1) и (F2) получим следующее уравнение: Pман · π d1²/4 = ρgh · πd2²/4, умножив обе стороны равенства на 4/ π и выразив h, получим: h = Pман · d1²/d2²/ρg. Подставим заданные значения в полученную формулу, для этого значение манометрического давления переведем в Паскали, а значение диаметров в метры: Pман  = 3(кг/см²) = 294300(Па); d1 = 0,2м; d2 = 0,45м.

Отсюда: h = 294300 · 0,2²/0,45²/1000 ·9,8 = 5,93м.

Ответ:  Прямодействующий паровой насос при заданных параметрах может поднять воду на высоту равную 5,93м.

2 раздел: Гидродинамика

2.1 Задача 16 в-9

На водопроводной трубе диаметром  d1 установлен водомер диаметром d2. На какую высоту h2 поднимается вода в пьезометрической трубке, присоединённой к суженному сечению, при пропуске расхода Q, если уровень воды в пьезометре, присоединённом к трубке равен h1. Потери напора не учитывать.

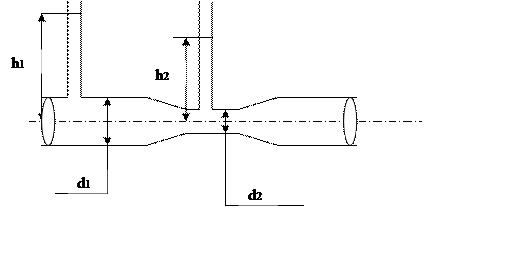Исходные данные: d1 = 75мм; d2 = 40мм; h1 = 0,8м; Q = 3л/с

Решение:

Для решения данной задачи нам необходимо воспользоваться уравнением Бернулли: Z1 + Р1/j + α1V1²/2g = Z2 + P2/j + α2V2²/2g. Выберем плоскость сравнения и два сечения и проанализируем величины в них. Плоскость сравнения выбирается произвольно, поэтому выберем её для удобства совпадающей с осевой линией и обозначим (0;0). Сечения возьмём рядом с пьезометрическими трубками на разных диаметрах трубопровода и обозначим соответственно (1;1) и (2;2).